摘要:数学以实践为源头, 又以实践为终结, 扎实的数学理论知识和灵活的数学思维, 都是为了将数学知识运用于解决实际问题中, 形成合理的思维模式。初二, 学生学习有关三角形的几何证明题, 做题的时候, 我发现许多学生不能把理论和实际操作有效的结合, 证明思维混乱。因此本文仅对初中二年级下册《有关三角形全等的几何证明题》思维模式作一探讨和总结。
关键词:初中数学; 几何证明;
1 正向思维:分析题目中的每一个重要条件, 产生结果, 寻找关系入口, 逼近问题
1.1 已知线段相等, 怎样用
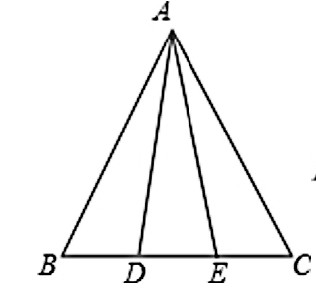
例1:已知如图1, 在△ABC中, AB=AC, 点D, E在边BC上, 且BD=CE.求证:∠ADE=∠AED.
图1
图2
分析:已知线段AB=AC, 标在图上观察, 这两条线段集中在同一个三角形中, 那么等边推等角, 得到∠B=∠C.已知线段BD=CE, 标在图上观察, 这两条线段没有集中在同一个三角形中, 那么找三角形, 证明ΔABD和ΔACE全等。得到AD=AE, AD、AE这两条线段在同一个三角形中, 等边推等角∠ADE=∠AED.或由全等得到∠ADB=∠AEC, 再去推导∠ADE=∠AED.
1.2 已知线段的垂直平分线, 怎么用
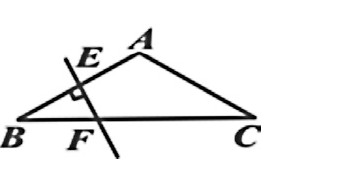
例3:如图2, 在ΔABC中, AB=AC, ∠BAC=120°, EF为AB的垂直平分线, EF交BC于F, 交AB于E.求证:CF=2BF.
分析: (1) 、AB=AC, ∠BAC=120°知道∠B=∠C=30°, 这里许多学生一下子可能考虑不到AB=AC跟∠BAC=120°之间的关系, 教师可引导学生逐步分析、发现、总结; (2) 、EF为AB的垂直平分线, 优先考虑特征, 连接AF, 则AF=BF, 一条线索走到底, 那么∠BAF=∠B=30°, 则∠FAC=120°-30°=90°, ∠AFB=120°、∠AFC=60°;在直角ΔAFC中, ∠C=30°, 敏感30°所对的直角边等于斜边的一半, 因此AF=CF, 转化为2倍关系则CF=2AF, 即CF=2BF.
1.3 已知角的角平分线, 怎么用
已知角平分线, 要么“走定义”, 要么“走特征”.定义:给两个小角“起名字”∠1, ∠2等等, 则两个小角相等, 等于大角的二分之一。特征:角平分线上的点到这个角的两边的距离相等。
2 逆向思维:从问题出发, 推导分析, 向已知条件靠拢
2.1 求证两条线段相等, 怎么操作
基本方法:若求证的两条线段没有在同一个三角形中, 那么可以围绕求证的两条线段找三角形, 证明三角形全等。若求证的两条线段, 在同一个三角形中, 也可以通过证明等腰三角形来说明这两条线段相等。
其他方法:求出这两条线段的长度;或借助“中间关系”, 例如找第三条线段, 证明这两条线段都与第三条线段相等。或借助“方向”, 例如借助要求证的这两条线段所在的“方向”, 证明还存在两对其他线段上的相等关系, 通过“加”或“减”再证明这两条线段相等。
2.2 求证两个角相等, 怎么操作
基本方法:若这两个角没有在同一个三角形中, 那么围绕这两个角找两个三角形, 证明全等。若这两个角在同一个三角形中, 那么也可以证明等腰三角形来求证这两个角相等。
其他方法:求出这两个角的度数;或借助“中间关系”, 例如找第三个角, 证明这两个角都与第三角存在关系。或借助“平行关系”由两直线平行推导“三类角”, 例如两直线平行, 同位角相等;两直线平行, 内错角相等。
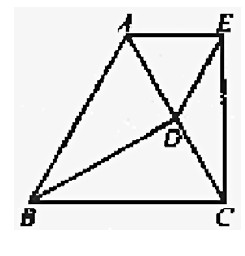
例2:如图3, D是等边ΔABC的边AC上的一点, 且BD=CE, ∠ABD=∠ACE.求证:⑴、ΔADE是等边三角形。⑵、∠DBC=∠DEC.
图3
图4
分析⑴:已知等边ΔABC, 则AB=AC=BC, ∠BAC=∠ACB=∠CBA=60°;已知BD=CE, 标在图上观察, 这两条线段没有在同一个三角形中, 找三角形证明ΔABD和ΔACE全等;已知∠ABD=∠ACE, 标在图上观察, 这两个角度没有在同一个三角形中, 则还是指向证明ΔABD和ΔACE全等。用SAS证明全等, 得到AD=AE, ∠BAD=∠CAE=60°;最后证明ΔADE是等边三角形。
⑵:“走关系”重新加工的方法。已知∠ABD=∠ACE, ∠ABD、∠ACE都是60°的一部分, 则60°-∠ABD=60°-∠ACE即∠DBC=∠DEC. (求证∠DBC=∠DEC, ∠DBC是60°的一部分, ∠DBC=60°-∠ABD=60°-∠ACE.观察图, 外角定理60°-∠ACE=∠DEC.所以∠DBC=∠DEC.)
2.3 求证线段的垂直平分线, 怎么操作
第一种做法:定义。既证明垂直, 又证明平分。
第二种做法:特征的逆定理。到一条线段两个端点距离相等的点, 在这条线段的垂直平分线上。
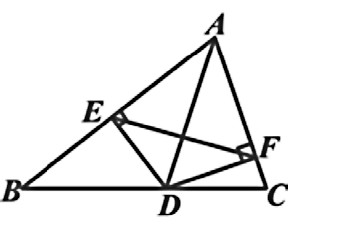
例4:如图4在ΔABC中, AD平分∠BAC, DE⊥AB, 垂足为E, DF⊥AC, 垂足为F.求证:AD垂直平分EF.
分析:已知AD平分∠BAC, 走定义∠BAD=∠CAD, 走特征ED=FD.不论走定义还是走特征, 都能证明ΔAED和ΔAFD全等, 得到AE=AF, 所以点A在线段EF的垂直平分线上。因为ED=FD, 所以点D也在线段EF的垂直平分线上, 因此AD垂直平分EF.
第二种做法:考虑定义的证明方法。
2.4 求证角平分线, 怎么操作
第一种做法:定义。证明两个小角相等。
第二种做法:特征的逆定理。到角平分线两边距离相等的点, 在这个角的角平分线上。
理论和实践的结合, 靠的就是思维。有了正确的思维方法, 可收到事半功倍的效果, 只要学生掌握了思维模式方法, 就不会做一些盲目、无效的劳动, 而是有的放矢、自觉地运用总结、归纳出的方法解决问题, 就会少走很多弯路, 把学习活动变成一种有目的、有意识、有趣味的活动, 使学生善思、乐学, 体会数学的情趣。