高中解题中数形结合理论的运用分析

　　【摘 要】
　　
　　本文主要探究数形结合思想在高中数学解题中的应用，概述数形结合思想以及数与形之间的相互转化，并结合经典数形结合的例题进行了初步研究。
　　
　　【关键词】
　　
　　数形结合；思想方法；高中数学。
　　
　　1何为数形结合

      数形结合思想，作为高中数学最基本的思想方法之一，它渗透在各个章节里，直观的感受让我们形成了对事物的感性认识，为我们加深理解数学定义和性质打下了基础，所以说数形结合思想是研究数学问题的一个非常重要的思想方法。
　　
　　数形结合思想是一种很重要的数学思想，强调数和形的结合，就是对题目的条件和结论，在分析其代数与几何的结合上找出其解题思路。形和数这两个基本概念，是数学的两块基石，在数学教学中，全部教学大体上都围绕着这两个概念的提炼、演变、发展而展开的，在数学教学发展的过程中，形和数常结合在一起，在内容上互相联系，在方法上互相渗透，在一定条件下互相转化。 本来，在现实世界中，形与数是不可分离地结合在一起的，这是直观与抽象的结合，感知与思维相结合的体现。形与数相结合不仅是数学自身发展的需要，也是加深对数学知识理解、发展智力、培养能力的需要。
　　
　　下面就数形结合思想在函数、不等式、线性规划及解析几何中的应用做一个初步的探究。
　　
　　2数形结合思想在高中解题中的相关应用

      2.1 解决函数问题

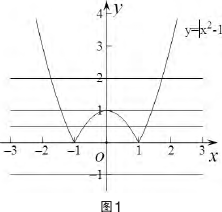
      例 1 设方程|x2-1|=k+1,讨论 k 取不同的值时其不同解的个数的情况。
　　
　　解：我们把这个问题转化为确定函数 y1=|x2-1|与 y2=k+1 图像的交点的个数的情况，因为函数 y2=k+1 表 示平行于 x 轴 的所有直线，从 图像六可以直观的看出：
　　
　　①当 k<-1 时，y1与 y2没有交点，这时原方程无解。
　　
　　②当 k=-1 时，y1与 y2有两个交点，原方程有两个不同的解。
　　
　　③当-1<k<0 时，y1与 y2有四个不同的交点， 原方程不同解的个数有四个。
　　
　　④当 k=0 时，y1与 y2有三个交点，原方程不同解的个数有三个。
　　
　　⑤当 k>0 时，y1与 y2有两个交点，原方程不同解的个数有两个。
　　

　　2.2 解决不等式问题例 2 已知 a>1,解关于 x 的不等式 ax+12>|x-1|.
　　
　　在同一坐标系中，作 y1=ax+12和 y2=|x-1|的图像，如图 2.