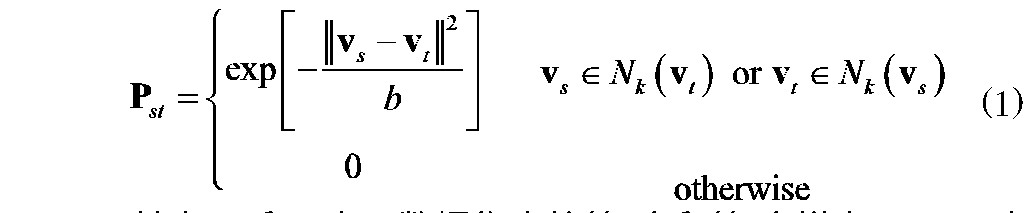摘要:针对离散数学课程的课时短、难度大导致的学生学习兴趣不足, 效率低下, 教学效果不理想的问题, 本文提出了一种理论结合科研实际的离散数学教学方法, 以达到培养学生自主学习动力, 激发学生学习兴趣的目的。在理论授课的同时, 结合科研实际中离散数学的具体应用, 对离散数学中的数学定义和具体应用进行类比分析, 提高学生的感知认识, 实现教学质量的有效提升。
关键词:离散数学; 类比分析; 教学方法;
Exploration on the Teaching Method of Discrete Mathematics in Combination with the Practice of Scientific Research
Abstract:Focusing on the problem of short time and difficult to grasp of discrete mathematics curriculum, which results in lacking interest in learning of the students, inefficiency and unsatisfactory teaching effect, this paper puts forward a discrete mathematics teaching method based on scientific research combing the theory so as to cultivate the students' autonomous learning power and achieve the final goal of stimulating students learning interest. Along with the theoretical teaching, the practical applications of discrete mathematics are introduced into the classes, the analogical analysis of mathematical definition and specific application in discrete mathematics are carried out to improve the students' perception. Effective improvements of teaching quality can be obtained with satisfactory.
Keyword:Discrete Mathematics; analogical analysis; teaching method;
0、引言
离散数学 (Discrete Mathematics) 是计算机专业的一门专业基础课, 在计算机科学中有着重要而广泛的应用, 是计算机专业课--数据结构、操作系统、编译原理、数据库和算法分析等课程的先导基础课程。此外, 其还是计算机科学与技术、软件工程、通信工程、电子信息工程、电磁场与微波技术以及智能科学技术等计算机类、信息类本科专业的核心基础课程之一。目前, 离散数学已经在当下流行的机器学习、模式识别和图像处理等科研领域中起到了重要的数学支撑作用。
鉴于离散数学的重要作用, 如何让相关专业学生掌握其精髓至关重要, 需要相关领域学者从教学内容、教学方式等方面不断地开拓创新。本文提出一种在教学中结合相关科研实际的教学方法, 以期化繁为简, 达到深入浅出地传授离散数学中的理论知识点, 激发学生的兴趣, 提高教学质量的目的。理论结合实际的教学方法既提高了学生的理论水平, 又为后续学生攻读硕士研究生和博士研究生打下科研基础, 可大幅度提高学生利用数学知识解决实际问题的兴趣和能力。
1、面临的困难
离散数学具有难度大和课时短的特点, 虽然已经有诸多有效的教学方式和方法被提出, 但在实际教学过程中可以发现, 虽然同学们的学习热情和理解能力确实取得了一定程度的进步, 但距离预期的目标仍然较远, 学生的自主学习热情和动力仍然不足, 对概念和定义的理解仍然不够透彻。
根据教育部“离散数学”教学指导委员会的建议, 国内离散数学的教学大致可以分为科学型、工程型和应用型三种类型, 每种类型对应的学时分别为108个学时、90个学时和72个学时。然而, 在实际的教学过程中, 离散数学的教学课时量常常会被压缩, 一般正式授课时间约为48学时, 我校为54学时。如何在有限的时间里把大量知识点传授给学生, 并同时将能力传播给学生, 给“离散数学”的教学提出了严峻的挑战。通过减少学时数量、降低考试难度的途径则会南辕北辙, 使得学生无法认识到“离散数学”在个人专业建设上的重要地位。
离散数学由于其本身的数学性质, 难度较大。若在实际教学中, 把“离散数学”作为一门数学课进行授课, 采用数学系老师采用的“定义-定理-证明-习题”的教学模式, 则严重忽视了“离散数学”的实际应用背景, 导致学生本能的厌恶与排斥, 降低了学习兴趣, 最终影响教学质量。
面对这些困难, 在离散数学的教学过程中急需寻找新突破来改善离散数学的教学方法。想要激发学生的主动性和兴趣, 必须加强理论联系实际的环节。
2、理论讲授与实际应用的结合
如前所述, 教师很容易把离散数学课程当成数学课来处理, 只讲定义、概念和理论, 而对这些知识的实际应用背景则介绍甚少, 甚至完全不涉及。想要提高学生的学习积极性, 授课必须结合相关领域的实际应用背景进行, 这样才能提高教学的针对性, 使学生觉得学有所用, 激发兴趣。那么研究如何为离散数学的各部分教学内容找到应用的实例, 是理论结合实际的重中之重。
教师将其自身的科研及学科前沿的课题引入教学中是一种极佳的途径, 因为教师对自己的课题研究时间和深度都足够, 对其有深入的理解, 因此可以深入浅出的结合离散数学中的定义和概念。这样就可以使学生尽早接触科研, 使学生们的科研能力得到锻炼, 学生不仅掌握基础理论, 而且培养了学生的科研能力和科研兴趣。以下通过本课题组科研项目中用到的一个较为简单的科研实例对图论部分的基础定义和概念开展分析。
2.1模式识别中图模型的构建
2.1.1图的基本概念
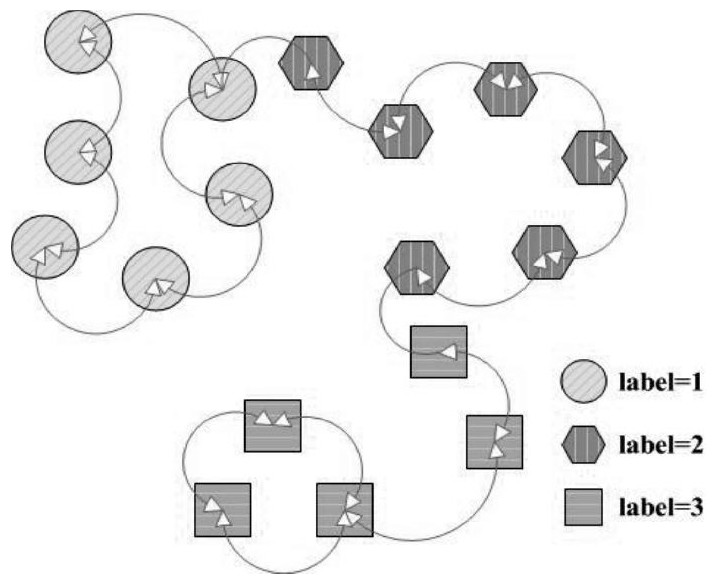
无向图:边没有方向的图。
连通:在某个已知的无向图里, 从图中的某一点a到另一点b或者从b到a之间存在一条路径, 便称a和b之间为相互联通的。
单纯的定义无法使学生产生直观的认识, 更无法意识到这些定义对实际的工程实践与科学研究有什么意义。结合实际应用开展分析与教学可达到事半功倍的效果。
2.1.2模式识别中图的使用
在模式识别领域中, 如何捕获数据结构, 并保持降维前后数据的本质结构对高精度识别至关重要。为此国内外学者付出了诸多努力, 一种有效的方式为将流形学习理论引入到模式识别的框架中, 其通过近邻矩阵的构建描述数据的局部结构。将近邻矩阵的每一个元素建模为以下形式:
通过这个简单的例子, 既可以让学生从枯燥的数学定义中摆脱出来, 而且也使得学生对于图的理解不再简单地停留在概念上, 可使得学生不再困惑所学究竟为何用。事实上, 更复杂的图模型的使用可能会使学生对概念的理解更加清晰, 因为更复杂的图模型会引入更细节的把握, 但也有可能使得学生陷入背景问题而脱离了离散数学本身, 因此我们暂时仅在教学中引入简单的图模型, 这样既提高了同学们的学习兴趣, 也达到了教学的目的。
3、结论
“离散数学”作为计算机大类专业的一门重要的专业基础课, 除了计算机领域, 其在诸多电子信息相关领域也具有广泛的应用。本文提出了在教学时结合相关科研领域中的实际应用例子, 深入浅出地传授和讲解“离散数学”中的知识点, 采用理论教学结合科研实践的思路, 唤醒学生的学习动力, 激发学生的主动学习兴趣, 从而提高教学质量, 使学生的理论水平和科研能力都得到有效的提高。
参考文献
[1]莫愿斌。凸显计算机专业特色的离散数学教学研究与实践[J].计算机教育, 2010.7:111-113.
[2]屈婉玲, 王元元, 傅彦, 等。“离散数学”课程教学实施方案[J].中国大学教学, 2011.1:39-41.
[3]李艳玲, 张剑妹。基于建模能力培养的离散数学思维模式[J].计算机教育, 2014.4:76-79.
[4]邓秀勤, 郝志峰, 刘海林。基于创新能力培养的离散数学课程教学改革探索[J].计算机教育, 2013.16:62-66.
[5]常亮, 徐周波, 古天龙, 等。离散数学教学中的计算思维培养[J].计算机教育, 2011.7:90-94.
[6]王瑞胡。应用型本科院校计算机专业《离散数学》实践教学改革研究[J].现代计算机, 2010.3:60-64.
[7]黄震。《离散数学》课程在计算机学科中的作用及其应用[J].赤峰学院学报:自然科学版, 2011.5:264-265.
[8]傅允准。课程实践教学的改革实践与创新人才的培养[J].上海工程技术大学教育研究, 2009.4:6-9.