“离散数学”求解关系的传递闭包方法

　　摘    要：　“离散数学”是计算机相关专业的核心课程，而关系是“离散数学”中刻画事物间内在规律性的数学模型，是数据结构及数据库等很多后续课程的基础。由于在关系中，求解关系的传递闭包，是学生普遍比较难掌握的内容，也是出错最多的地方，本文基于此背景介绍了求解关系的传递闭包的四种方法，并对同一个关系闭包问题的四种方法进行比较，这些方法虽然都能用来很好地求解关系的传递闭包，但是关系图法最为适用，学生比较容易掌握，从而有效提高了教学质量。

　　关键词 :     离散数学,关系;传递闭包:

　　Abstract：　Discrete mathematics is the core course of computer-related majors, and relationship is a mathematical model that depicts the inherent regularity between things in discrete mathematics and is the basis of many subsequent courses such as data structures and databases. Because in the relationship, solving the transitive closure of the relationship is generally more difficult for students to master, and it is also the place with the most mistakes. Based on this background, this article introduces several methods for solving the transitive closure of the relationship and compares the four methods of the package problem of the same relationship. Although these methods can be used to solve the transitive closure of the relationship, they are most suitable for the relationship graph method. The students are particularly easy to master, which effectively improves the quality of teaching.

　　Keyword：　discrete mathematics; relations; transitive closures; sets;

　　1、 引言

　　“离散数学”是计算机相关专业的一门专业基础课，其教学内容与高校数学专业课程极为密切，但学习该课程的大多为计算机相关专业学生，该门课程也是许多课程必不可少的先行课程，如操作系统、数据结构、程序设计、数据库、人工智能、算法设计与分析等[1]。学生通过学习“离散数学”课程，可以掌握处理离散结构的描述工具和方法，提高逻辑推理能力和抽象思维能力[2]。

　　众所周知，关系是“离散数学”中刻画事物间内在规律性的数学表示，“离散数学”中所有的内容都可以用关系进行描述，关系在数学领域有重要作用，广泛应用于计算机科学技术中，而且关系也是数据结构及数据库等很多后续课程的基础[3]。在数学中，表示两个元素间的关系称为“二元关系”,简称“关系”。设A,B为集合，A×B的任意子集叫做A到B的二元关系，它是一个二元组的集合，即R={(x,y)/x∈A,且y∈B}。特别当A=B时称为集合A(或B)上的二元关系[4]。学生在初学关系时，会感到特别困难，主要是关系中的定义和定理过多，而且定义比较抽象，因为“离散数学”课时本来就不是很多，那么分配到关系上的课时就更少了，对关系的闭包的学习是很粗略的，求关系的传递闭包是学生普遍难掌握的，也是出错最多的。所以本文介绍几种求定义在有限集合上的关系的传递闭包的方法[5]。

　　给定一个二元关系R,它不一定具有某种性质(比如自反性、对称性、传递性),而我们又想让它具有这些性质，就需要在关系R中添加一些二元组构成一个新的关系，使它具有我们需要的性质，但是又希望添加最少的二元组，即添加的二元组尽可能得少[6]。通过这样的方法产生新的关系，就是关系的闭包运算，主要有三种闭包：自反闭包r(R)、对称闭包s(R)、传递闭包t(R)。学生对自反闭包和对称闭包的求法掌握很好，基本都能正确求出，而对传递闭包的计算，大多数同学感觉很难，如果是关系R比较简单，涉及到的二元组比较少，大部分同学还是可以求出来的，但是对于稍微复杂点的关系，学生求传递闭包的时候，不是少添加了一些二元组，就是添加了一些不必要的二元组[7]。

　　2 、求解关系的传递闭包方法

　　2.1、 定理法

　　定理1 设关系R是集合A上的二元关系，|A|=n≥1, 则R的传递闭包[8]

　　t(R)=∪i=1nRi=R1∪R2∪R3∪...∪Rn,

　　例如，集合A={a,b,c,d}, A上的二元关系R={(a,a),(a,b),(b,a),(b,c),(c,d)},利用定理1求关系的传递闭包，

　　R2={(a,a),(a,b),(a,c),(b,a),(b,b),(b,d)},

　　R3=R2。R={(a,a),(a,b),(a,c),(b,b),(b,c),(a,d)},

　　R4=R3。R={(a,a),(a,b),(a,c),(a,d),(b,a),(b,b),(b,c),(b,d)},

　　t(R)=R∪R2∪R3∪R4={(a,a),(a,b),(b,a),(b,c),(c,d),(a,c),(b,b),(b,d),(a,d)},

　　以上用到了关系的复合运算：

　　定义1[8] 设A,B,C是集合，若R?A×B,S?B×C,则关系R与关系S的复合R。S定义为：R。S={(x,z)|x∈A,z∈C,?y∈B,使得(x,y)∈R,(y,z)∈S}[4] 。

　　以上利用定理1求关系的传递闭包的方式繁琐，如果集合A中元素个数太多，则计算量过于大了。

　　2.2、 观察验证法

　　在关系R中观察，如果存在类似(x,y),(y,z)的二元组，则在R中添加二元组(x,z)然后验证关系R是不是具有传递性，如果具有传递性，则添加二元组后的关系R就是传递闭包t(R),否则，继续在R中添加二元组，再进行验证，直到R具有传递性为止。

　　例如集合A={a,b,c,d},A上的二元关系：

　　R={(a,a),(a,b),(b,a),(b,c),(c,d)},

　　现在利用方法二求关系的传递闭包。

　　通过观察，我们可以发现

　　(b,a)∈R,(a,b)∈R,(a,b)∈R,(b,c)∈R,(b,c)∈R,(c,d)∈R

　　所以可以在R中添加二元组(b,b),(a,c),(b,d)。此时，关系

　　R={(a,a),(a,b),(b,a),(b,c),(c,d),(b,b),(a,c),(b,d)},

　　现在利用下面的定理2验证R是不是具有传递性，因为

　　R。R={(a,a),(a.b),(a,c),(a,d),(b,a),(b,b),(b,c),(b,d)}?R,

　　所以此时R不具有传递性，再观察此时的关系R,可以发现

　　(a,b)∈R,(b,d)∈R,或者(a,c)∈R,(c,d)∈R,

　　所以需要再添加二元组(a,d),此时

　　R={(a,a),(a,b),(b,a),(b,c),(c,d),(b,b),(a,c),(b,d),(a,d)},

　　现在再次利用定理2验证R是不是具有传递性

　　R。R={(a,a),(a.b),(a,c),(a,d),(b,a),(b,b),(b,c),(b,d)}?R,

　　所以此时R具有传递性。

　　定理2[8] 设R?A×A,则R在A上传递的充要条件是R。R?R。

　　2.3 、关系图法

　　利用关系图的方法来求传递闭包，就不会漏掉一些二元组，介绍该方法之前，先介绍与之相关的两个概念：(1)如果顶点vi到顶点vj没有直接的有向边连接，但是却可以通过其他有向边相通，即顶点vi顶点vj之间存在通路，则称顶点vi与顶点vj是可达但不是可直达的；(2)如果顶点vi与顶点vj存在有向边<vi,vj>,则称顶点vi与顶点vj是可直达的。显然，两个顶点之间可直达必可达，但是可达不一定可直达[4]。

　　该方法的算法如下：

　　设关系R是集合A上的关系，|A|=n,在关系R的关系图中，判断任意两个顶点vi到vj是否可达?

　　(1) 若顶点v1到任意顶点vi(i=1,2,3,...,n)是否可达，如果可达，再判定是否可直达，如果可达但不可直达，则添加一条直达的边<v1,vi>。类似的，对于A中所有的顶点，都判定与所有顶点的关系。

　　(2) 其他情况(可直达与不可达),都不需要再添加边。即若两个任意顶点vi、vj不可达，则不需要添加边，若两个任意顶点vi、vj可直达，也不需要添加边[4]。

　　举例说明如下：

　　设集合A={a,b,c,d},A上的二元关系

　　R={(a,a),(a,b),(b,a),(b,c),(c,d)},

　　R的关系图如图1所示，求关系R的传递闭包t(R)。

　　图1 二元关系R的关系图

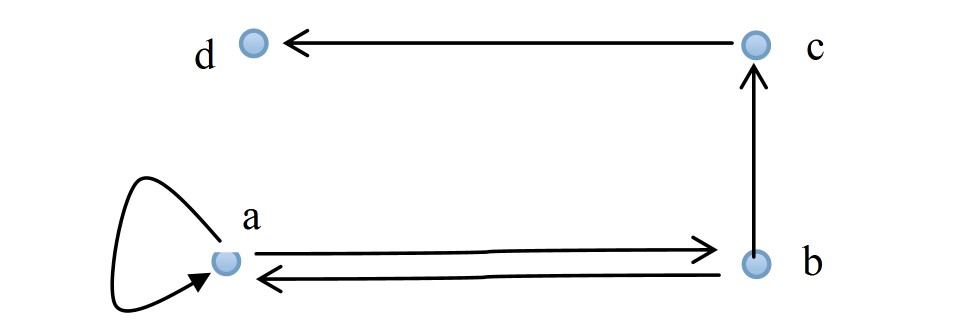
　　分析如下：

　　(1)检查顶点a

　　a点可达a点，并且可直达a点(因为存在边(a,a)),所以不需要添加边；同理，a点可达b点，并且可直达b点，所以不需要添加边；a点可达c点，但是不可直达c点(因为不存在边(a,c)),所以添加一条直达的边(a,c);a点可达d点，但是不可直达d点，所以添加一条直达的边(a,d);

　　(2)检查顶点b

　　b点可达a点，并且可直达a点，所以不需要添加边；b点可达b点，但是不可直达b点，所以添加一条可直达的边(b,b);b点可达c点，并且可直达c点，所以不需要添加边；b点可达d点，但是不可直达d点，所以添加一条可直达的边(b,d);

　　(3)检查顶点c

　　c点不可达a点，所以不需要添加边；c点不可达b点，所以不需要添加边；c点不可达c点，所以不需要添加边；c点可达d点，并且可直达d点，所以不需要添加边；

　　(4)检查顶点d

　　d点不可达a点，所以不需要添加边；d点不可达b点，所以不需要添加边；d点不可达c点，所以不需要添加边；d点不可达d点，所以不需要添加边；

　　综上所述，可得

　　t(R)={(a,a),(a.b),(b,a),(b,c),(c,d),(a,c),(a,d),(b,b),(b,d)}。

　　2.4、 矩阵法

　　根据关系的矩阵也可以求出关系的传递闭包，给定有限集合A上的关系R,R的传递闭包的关系矩阵等于：

　　MR∞=MR∨MR2∨MR3∨...,

　　其中MR表示关系R的关系矩阵[6]。

　　设集合A={a,b,c,d},A上的二元关系

　　R={(a,a),(a,b),(b,a),(b,c),(c,d)},

　　则

　　MR　　而

　　这里?表示布尔矩阵的布尔积，因此有

　　MR∞=MR∨MR2∨MR3∨MR4

　　如果写成关系的集合形式如下

　　t(R)=R∞={(a,a),(a.b),(b,a),(b,c),(c,d),(a,c),(a,d),(b,b),(b,d)}。

　　3 、比较分析

　　将以上四种求解关系传递闭包的方法应用于实际教学中，通过对学生发放问卷和分析往年考试题目了解以上四种求解关系的传递闭包的方法在实际教学中的情况。

　　(1)计算机与信息工程学院2019级物联网工程专业和计算机科学与技术专业共199名同学进行问卷调查情况如下：

　　表1 学生运用求解关系传递闭包的方法的调查问卷结果

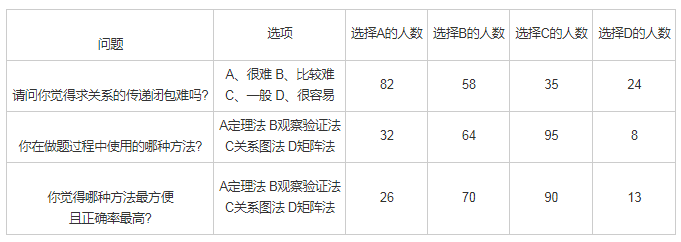
　　通过调查问卷分析表明，有41.2%的学生觉得求解关系的传递闭包很难，29.1%的学生觉得比较难，只有12.1%的学生觉得很容易。而在求解关系的传递闭包方法上，使用关系图法的学生有47.7%,采用观察验证法的学生有32.2%,运用定理法的学生有16.1%,利用矩阵法的学生有4.0%,由此可以看出，使用关系图法来求解关系的传递闭包的学生最多。有45.2%的学生觉得关系图法最方便且正确率最高，35.2%的学生觉得观察验证法最方便，13.1%的学生觉得定理法最方便，6.5%的学生觉得矩阵法最适合，由此表明，关系图法是在求解关系的传递闭包中最受学生喜欢的一种方法。

　　(2)近两年计算机与信息工程学院开设“离散数学”课程的四个专业共523人的期末考试试卷中求解关系的传递闭包的考试题目统计分析情况。

　　表2 近两个学年期末考试卷中求解关系的传递闭包的考试题目统计分析表

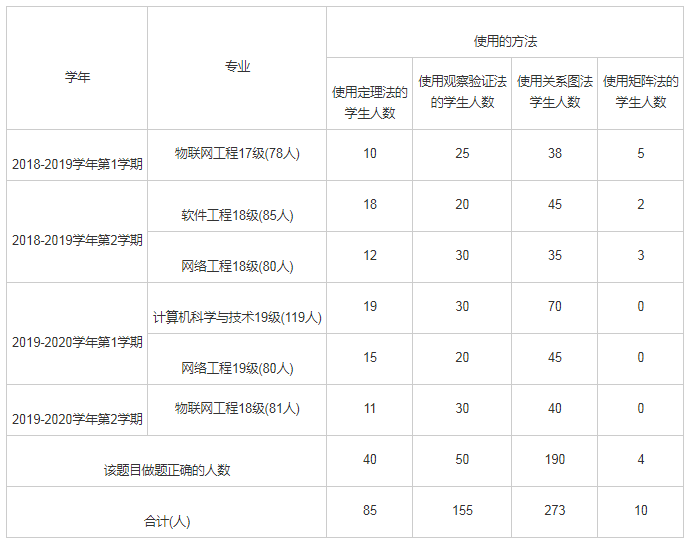
　　由表2说明，学生在求解关系的传递闭包时使用关系图法的人数达到52.2%,正确率为69.6%,采用观察验证法的学生占29.6%,正确率为32.2%,运用定理法的学生占16.2%,正确率为47.0%,利用矩阵法的学生占2.0%,正确率为40.0%,这表明关系图法是在求解关系的传递闭包中最受学生喜欢的一种方法，并且正确率也是最高的。

　　4 、结语

　　本文介绍了求关系的传递闭包的几种方法，从这些方法的介绍和应用中，可以看出：定理法比较繁琐，需要对关系的复合运算掌握特别熟练，并且如果集合A中元素个数太多，则计算量过于大了。而观察验证法的优点在于比较直观，但是其缺点是最容易漏掉一些二元组。相对于观察验证法而言，关系图法虽然不容易漏掉二元组，但是却需要学生对图论知识的掌握比较熟练。矩阵法就比较直观，只需要学生有良好的代数基础，要对其中的矩阵计算很熟练。以上几种方法都在近两年计算机专业学生“离散数学”中关系传递闭包的实际教学中进行了教学和总结，通过学生学习关系传递闭包的课堂表现、课堂作业练习效果和期末考试试题分析表明关系图法最为容易接受和理解，并能准确地应用于求关系传递闭包，这大大提高了教师的课堂教学质量和学生的学习效果。

　　参考文献

　　[1]刘贵龙从关系传递闭包算法的教学看学生创新能力的培养[J].计算机教育, 2016(12):54-56+63.

　　[2]屈婉玲，玩玩,傅彦，等"离散数学”课程教学施方案[J].中国大学教学, 2011(1):39-41.

　　[3]付丽.二元关系传递性的判定[J]绥化学院学报。2011,31(2):184- 186.

　　[4]匡能晖，胡国辉离散数学教学中采取的三点技巧[J].当代教育理论与实践，2011(9):71-73.

　　[5]张从文二元关系传递闭包的实现算法[J]电脑编程技巧与维护, 2020(3):50-52.

　　[6]刘玉珍,李雄,朱萍,等几种求解有限集合上传递关系闭包方法研究[J]教育现代化, 2018,5(26):150-152.

　　[7]孙凤芝有限集上二元关系传递闭包的构造[J]大庆师范学院学报, 2009 29(6):44-47.

　　[8]邓辉文离散数学[M].北京:清华大学出版社, 2019,35-61.