离散数学“KM教学+计算思维”教学模式分析

　　1 研究背景

　　离散数学的课程改革现在已经越来越普及，KM教学作为一种新的教学方法改革也已慢慢应用在离散数学的知识体系结构中，而计算机教育中我们所关注的计算思维能力的培养能否在这种教学模式中得到体现呢？计算思维和思证思维、逻辑思维一样，必定会成为一个现代公民必须掌握的基本思维模式，而计算思维能力的培养，首先要建立计算的基本意识，了解计算的基本功能，掌握计算的基本方法，会用计算的基本工具，具备计算的基本能力。离散数学的学习过程中我们将内部逻辑结构与思维导图相融合，运用计算思维的方式引导学生学习问题求解和知识发现，通过抽象模型的建立以获得问题的求解。

　　2 “KM 教学+计算思维”的课程教学

　　离散数学基本内容包含数理逻辑，集合和关系，代数系统和图论，教学中以离散数学的知识逻辑结构作为核心，通过思维导图演绎，把四大篇内容按照知识点的内在逻辑性，建立知识的逻辑结构图，我们采取先把结构搭建，再充实细节，最后加以融合贯通。而在讲授过程中，我们采用最基本的问题描述方法（符号化，模型化），最主要的思维方法（抽象思维，逻辑思维），最基础的实现形式（程序，算法，问题表示，数据结构，系统实现），最典型的问题求解过程（问题，形式化描述，计算机化），而这些都可以称之为“计算思维”[1].学习离散数学就是增强学生的逻辑思维能力和利用离散结构来构建问题的抽象数学模型能力，进而在这个构建的模型上解决问题的能力。而这种能力就是计算机专业的学生具备计算思维能力的重要体现。

　　具体实例如下：在集合与关系篇中，我们首先介绍了集合的性质和运算，然后引入笛卡尔积来说明关系是由集合与集合的运算所生成，接下来再介绍关系的表示、关系的性质和关系的运算[2].这样从浅到深、从抽象到具体、从简单到复杂、从定义到运算再到组合成新的复杂关系（偏序关系和等价关系），我们根据信息加工理论来展现这种多层次的逻辑结构。这一节中关系的表示、运算和性质作为横向知识结构定义，然后纵向上再深化为具体的表示（关系图，序偶对和关系矩阵），具体的运算（复合运算，逆运算和闭包运算），具体的性质（5条性质），环环相扣展开铺垫，最终形成关系这张知识网络结构图[3].这就是我们所说的KM教学法，下面给出了关系的一个思维导图，如下图图1所示。

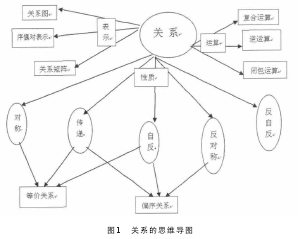
　　从计算思维的角度来看，我们可以把关系的五条性质抽象成符号表示，借助符号推理来判断生活中任何一个关系具备哪些性质。而派生出来的两种复杂关系等价关系和偏序关系的区分和联系又是什么？采用基于计算思维的任务驱动模式设计教学流程[4],就可以从思维方法的高度去培养学生，使学生能够具备从实际应用中抽象得到问题、分析问题以及运用所学知识解决问题的能力。

　　3 效果跟踪评价

　　为了验证这种“KM教学+计算思维”教学模式对学生的学习效果和思维能力培养的效果，我们改变了原有的学业成绩评价模式。传统考核方式主要依靠考勤的记载和期末卷面分来评价学生掌握知识的程度，由于学生通常临阵磨枪，强化训练，最终头脑中形成的是对知识的瞬间记忆和强化复制，并没有达到我们希望学生具备的解决问题的能力。所以我们采用多手段多方式教学评价，最终考查学生是由平时课堂互动、习题解答、期中考试、通过网络教学平台自主化学习能力和期末考试等多渠道考查模式，最终的评价结果也可以量化为学生自己画出的KM思维导图、自己设计出的抽象数学模型、知识点具体应用在生活的案例等。同时我们采用的这种模式也在某种程度上积极调动了学生的积极性和学习能力的大幅度提升，学生由原来的被动式学习变成了主动式学习，监督式学习，同时提升了学生的计算思维和逻辑思维能力，学生对这门课程的满意度也上升了。

　　4 结束语

　　“KM教学法+计算思维”就是构建培养学生计算思维能力的一种教学模式，它解决了计算思维的基本内容如何表达，清楚地描述计算思维相关的知识内容及其之间的关系[5].这是一个计算机专业学生应该具备的能力，也是所有大学生应该具备的能力。这种思维的培养可以造就具有良好知识修养和自由独立精神，敢于创新，善于创新的应用型人才。

　　参考文献：
　　[1] 朱亚宗。论计算思维：计算思维的科学定位，基本原理及创新路径[J].计算机科，2009,（04）。
　　[2] 程虹。离散数学习题集[M].武汉大学出版社，2006.
　　[3] 程虹。KM教学法在离散数学课程中的创新应用[J].计算机光盘软件与应用，2014,（12）。
　　[4] 齐兴敏。项目驱动式教学法在离散数学教学中的应用探讨[J].现代商贸工业，2009,（15）。
　　[5] 廖志伟。李文敬等。基于培养学生计算思维任务驱动式“离散数学”教学模式[J].计算机教育，2009,（06）。