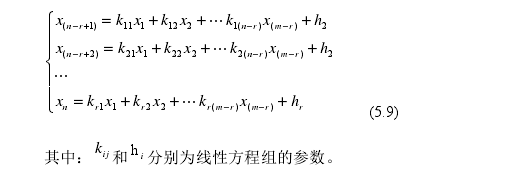第 5 章 LMN 公司产品成本控制模型应用分析 .
5.1 EOQ 模型在产品成本控制中的应用分析 .
通过对LMN公司产品成本控制现状的分析得出,LMN公司产品成本控制问题主要集中在研发环节成本控制、直接材料成本控制、质量成本控制等方面。从产品成本项目对产品成本控制的影响力来看,直接材料对产品成本控制的影响力最大,占有45%的比例,而直接材料成本的发生主要集中于原材料的采购过程与原材料的投入使用两个环节。基于LMN公司的实际情况,在采购环节引入了经济订货量模型来降低采购环节的成本;在生产环节引入投料比模型,确定合理的原材料投料比,从而降低LMN公司产品的成本,提高其产品成本控制水平。
5.1.1 建立 EOQ 模型 .
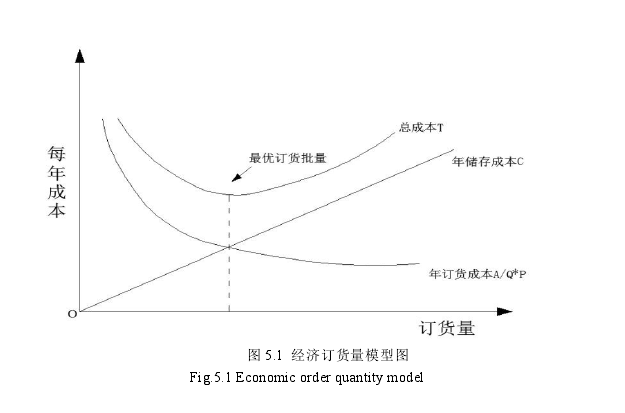
对于LMN制药公司来说,原材料是构成产品成本的重要成分,而怎样在确保正常生产的情况下,使所耗用的直接材料成本最低,一直是制药企业进行产品成本控制迫切追求的目标。本文针对LMN公司的采购条件,引用了EOQ经济订货批量模型,进而控制LMN公司的采购费用。本文所说的EOQ模型是指,在全年存货需求量已知的条件下,实现订货的储存成本与订货成本之和最小的状态时的订货量,根据求出的订货量计算出的成本即是最低的采购成本。运用EOQ模型可以有效解决LMN公司采购费用居高不下的问题,进而提高其采购环节的成本控制水平[40].EOQ模型图及具体公式如下:
5.1.2 EOQ 模型的应用分析 .
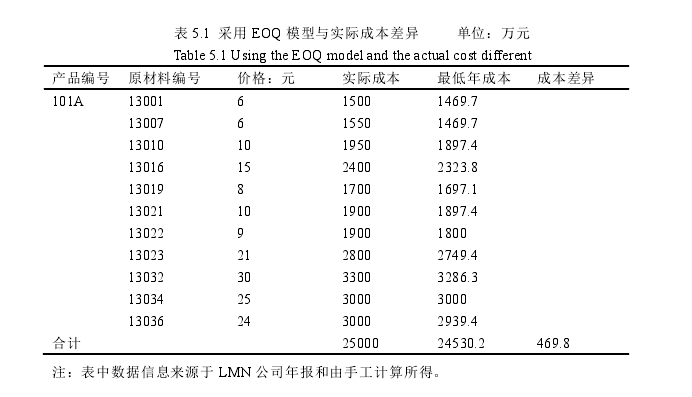
EOQ模型既能适用于控制LMN公司采购原材料的数量,也能用来合理控制其采购费用。LMN公司是河南省内新农合药品A产品的合作供应商之一,市场范围主要面向河南省内,年需求量基本稳定,根据LMN公司以前年度A产品的订单量,预计出的下年度订货量,A=10000万,把对仓储费用分摊至LMN公司生产的各产品中,求得A产品单位年存货成本C=18元,下表是实际生产10000万件的101A产品所耗费的各种材料成本与采用EOQ模型后的成本对比表。
通过上表可以看出,LMN公司应用EOQ模型进行原材料的采购时的采购成本为24530.2万元,而实际的采购成本为25000万元,低于实际成本费用469.8万元的成本,说明应用EOQ模型可以降低LMN公司的采购成本,解决其采购环节的采购费用居高不下成本控制问题。
5.2 投料比模型在产品成本控制中的应用分析 .
5.2.1 模型概述 .
当前LMN公司生产车间原材料的投入管理,主要侧重于对原材料供应链的管理,例如使原材料的供给能保证生产的顺利进行、降低原材料运输费用等。
LMN公司从原材料的供给、使用与采购物流成本三个方面控制其成本,但未涉及到原材料的投入配置方面的控制。对于LMN公司来说,原材料的配置不仅影响药品的成本,而且还会影响着产品的质量是否符合标准,从而增加产品的质量成本。由于LMN公司在直接材料成本控制方面还有可节约的限度,因此原材料的成本控制也是其进行产品成本控制重点项目之一。
LMN公司在生产中需要投入不同的原材料,例如:荆芥穗、薄荷、防风、柴胡、紫苏叶、葛根、桔梗、苦杏仁、蔗糖粉等多种原材料,而LMN公司根据生产计划进行产品的投料生产,对于某些某特定化学成分的药品生产时,各项原材料的投料方式可以有很多种,若要使其产品成本最小,则需对其所需原材料的投料方案进行计算。本文运用高等数学矩阵模型构造了某产品各项原材料消耗数量的模型[41],运用该模型的限制条件是产量一定,而LMN公司是河南省内某种药品的定点供应商之一,符合应用该模型的条件。该模型应用了拉格朗日乘数法与非齐次线性方程组等高等数学方法为基础开始探究,以产品的各项原材料投入量和其化学成分比例的对应关系作为研究对象,设立对应的非齐次线性方程组,求解此方程组,从而得到产品各项原材料消耗量之间的对应关系;在产品的生产量为限定条件的基础上,求解出最小的材料成本。运用矩阵模型,不仅可以准确计算产品的最佳配置比,而且可以在不同种类产品生产之前引入降低产品成本的矩阵分析模型,准确计算出产品的最佳投料比及最佳产品成本消耗的生产组合,为合理精确各项原材料的领料提供借鉴,降低不必要的成本浪费,从而降低产品的材料成本。
5.2.2 提出假设 .
针对原材料的配置模型提出如下假设:生产机器是生产部门计算产品产量、进行成本核算的工具,以生产部门的某台机器所生产的产品为目标进行研究。假设该生产机器的正常产量为Q,生产部门某机器的产量是关于其相应的各项原材料消耗量的函数。在机器产量与含有的化学成分已知的条件下,可以运用该模型精确计算出该产品原材料成本最低的原材料配置方案。
5.2.3 建立模型 .
设Q为某机器生产某种产品的产量,需要n中原材料,nxxx???21,是各种原材料的消耗量;单价分别为nbbb???21,;该产品含有m种化学成分,各种化学成分的含量分别为mccc???21,,根据各种原材料的消耗量和各种化学成分的含量关系,设立相应的高等函数矩阵方程组,如下:
此模型是在该生产设备的产量和所包含的各项化学指标一定的条件下设立的,对该矩阵方程(5.8)进行求解,得知该方程存在无数解,再根据各项原材料的投入数量,把方程的解带入该方程,从而求解出原材料成本最低时的情况,根据高等矩阵函数方程的特性,方程解的情况为:
再依据该生产设备生产的产品原材料的消耗数量及其单价又可以设立原料成本函数的方程,该方程如下:【图二十六】。
根据拉格朗日乘数法求极值的原则,整理后的函数可简化为:
5.2.4 结果分析 .
对高等函数所计算求得的结果进行分析可知,各项原材料的配置方法具有相关关系,符合生产部门的原材料配置原则,也遵守产品的质量准则。生产某种产品的原材料的配置不是任意的,相互之间有限制关系,遵循配置原则。由(5.13)可以看出,某些原材料的投入量与其他各项原材料之间的边际产量线性相关。最低原料成本配置方案包含各项原材料的边际产量,符合规定的配置规定,且该规定与对应的原材料的价格线性相关,也即因而,原材料价格变动会制约其配置比例。LMN公司的各种产品均可使用这种方法模型计算出成本最低的生产组合,在生产量确定的情况下,产品所耗用的原材料的量也即随之确定,这样可以控制领料人员合理领料,避免不必要的浪费。