2. 2研究工具
2. 2. 1心理弹性
采用胡月琴和甘怡群(2008) 编制的《青少年心理韧性量表》 ,共有27道题目,采用5点计分,从“1 =非常不符合”到“5 =非常符合”该量表包括目标专注、情绪控制、积极认知、家庭支持和人际协助五个方面,其中目标专注、情绪控制和积极认知属于个人力,家庭支持和人际协助属于支持力该量表是在心理韧性的过程模型下采取本土化思路编制成的,被证明有良好的信度和效度( 胡月琴,甘怡群,2008)本研究中,由于情绪控制维度与学校适应问卷中的自我控制和挫折耐受维度存在一定的重叠,且该维度与其他几个维度之间的相关比较低,因此删除了该维度的题目用其余维度下所有题目的平均值来代表个体心理弹性的总体情况在本研究中,第一年和第二年的克伦巴赫α系数分别为0. 70和0. 83.
2. 2. 2学校适应
采用Hightower等人(1986) 的教师-儿童评价量表,采用5点计分,从“1 =非常不符合” 到“5 =非常符合”.该问卷分为学校适应能力和学校适应问题两大部分,其中学校适应问题又包括内隐问题(9道题,例如,“忧虑、担心”)、外显问题(6道题,例如,“坐立不安,很难安静下来”)、学习问题(6道题,例如,“学习动机不强”)。由于学校适应能力中的自我控制和挫折耐受两个子维度与心理弹性的定义及测量存在一定程度的重叠,因此在此次分析中我们删除了这两个维度上的题目,只保留了亲社会行为(4道题,例如,“对同伴友好”)、社会性(6道题,例如,“有很多朋友”)、果敢社交(7道题,例如,“坚持自己的观点,不随大流”) 这3个子维度。该问卷最初为教师版,本研究中父母版本问卷在教师版本的基础上做了语言上的修订( 例如,将“上课时东张西望,做小动作”改为“学习时东张西望”) ,并增加了少量题目。 该问卷在中国文化中具有良好的信效度( 张光珍等,2013)。由于在中国文化中,学校适应能力的各个子维度之间具有较高相关,研究者通常将其合并作为一个单一的维度(Chen,Rubin,& Li,1995) ,因此本研究中计算学校适应能力的3个子维度下的所有题目的平均分作为学校适应能力的指标。在本研究中,学校适应能力、内隐问题、外显问题、学习问题两年的克伦巴赫α系数在0. 71 ~0. 95之间。
2. 3数据管理与统计分析
采用SPSS 17. 0 for Windows统计软件进行了数据录入与描述统计和相关分析,用Mplus 7. 0软件建立结构方程模型。
3、研究结果
3. 1描述统计与相关分析
各个变量的平均值、标准差、峰度、偏度及变量间的相关系数见表1,从表1可以看出,在第一年和第二年,心理弹性与适应能力存在显着正相关,而与学习问题、外显问题、内隐问题存在显着负相关。从第一年到第二年,心理弹性和学校适应各变量均存在中等程度以上的稳定性。无论是在第一年还是第二年,在外显问题、学习问题与学校适应能力上,父母报告的数据与教师报告的数据都具有中等程度以上的一致性,但是在内隐问题行为上,父母报告的数据与教师报告的数据的一致性较低。对父母和教师报告的学校适应各个变量的绝对水平进行了t检验,结果表明: 在第一年的学习问题 (t(826)= 4. 32,p < 0. 001)、外 显 问 题 (t(813)= 6. 01,p < 0. 001)、内 隐 问 题 (t(826)=5. 04,p < 0. 001) 和学校适应能力(t(857)= 2. 72,p < 0. 01) 方面均存在显着差异; 在第二年学习问题(t(836)= 4. 44,p < 0. 001)、外显问题(t(836)= 5. 23,p < 0. 001)、内隐问题(t(799)= 7. 17,p <0. 001) 和学校适应能力(t(857)= 2. 89,p < 0. 01)方面均存在显着差异; 父母报告的分数均高于教师报告的分数。
3. 2心理弹性与学校适应的纵向关系
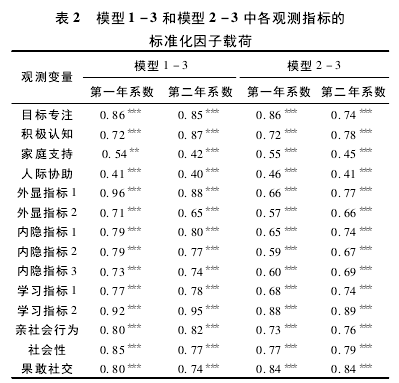
为了考察心理弹性与学校适应之间的纵向关系,用Mplus7. 0软件建立结构方程模型来进行分析。在建立全模型之前,我们先对心理弹性和父母及教师报告的学校适应建立测量模型,并建立第一年、第二年的测量等值模型。在基线模型中,包括第一年和第二年的心理弹性、外显问题、内隐问题、学习问题以及学校适应能力共10个( 第一、二年分别5个) 潜变量。其中,心理弹性有4个观测指标,即初中生报告的目标专注、积极认知、家庭支持和人际协助四个维度上的维度分; 学校适应能力包括3个观测指标,即教师( 模型1) 或父母( 模型2) 报告的亲社会行为、果敢社交和社会性三个维度上的维度分; 另外,将父母( 模型1) 或教师( 模型2) 报告的学校适应问题各维度下的题目打包,分别作为外显问题(2个数据包)、内隐问题(3个数据包) 和学习问题(2个数据包) 的观测指标。设定各个潜变量之间相关,允许各因子载荷自由估计。由于部分变量为非正态分布,因此我们采用稳健极大似然估计法(MLR) 来进行参数估计, 验证性因素分析结果显示,模型1(χ2= 744. 60,df = 294,χ2/ df = 2. 53,CFI = 0. 92,TLI = 0. 90,RMSEA = 0. 06,90% CI =[0. 05,0. 06],SRMR = 0. 06) 和模型2(χ2=588. 10,df = 292,χ2/ df = 2. 01,CFI = 0. 93,TLI =0. 91,RMSEA = 0. 05,90% CI =[0. 04,0. 05],SRMR= 0. 06) 都拟合良好。
接下来,我们分别以模型1和2为基础,限定同一个观测指标在第一年和第二年的因子载荷相等( 模型1 -1和模型2 -1)。验证性因素分析结果显示,模型1 - 1(χ2= 778. 93,df = 303,χ2/ df = 2. 57,CFI =0. 92,TLI = 0. 90,RMSEA = 0. 06,90% CI =[0. 05,0. 06],SRMR = 0. 06) 和模型2 - 1(χ2= 617. 49,df =301,χ2/ df = 2. 05,RMSEA = 0. 05,90% CI =[0. 04,0. 05],CFI = 0. 93,TLI = 0. 91,SRMR = 0. 06) 拟合良好,但是Δχ2达到了统计显着水平。因此,我们通过逐个去掉对因子载荷的限定来确定是哪个限定导致模型拟合变差,如果去掉限定之后卡方改变不显着,则仍然保留该限定,如果去掉限定之后卡方改变显着,则解除对该因子载荷的限定,最后得到模型1 - 2(χ2= 753. 11,df = 300,χ2/ df = 2. 51,CFI = 0. 92,TLI= 0. 90,RMSEA = 0. 06,90% CI =[0. 05,0. 06],SRMR = 0. 06) 和模型2 - 2(χ2= 601. 68,df = 299,χ2/ df = 2. 01,RMSEA = 0. 05,90% CI =[0. 04,0. 05],CFI = 0. 93,TLI = 0. 91,SRMR = 0. 06)。
接下来,我们分别以模型1 -2和模型2 -2为基础对教师报告的数据( 模型1 -3) 和父母报告的数据(2 -3) 建立全模型来考察心理弹性与学校适应之间的纵向关系。全模型的测量部分与模型1 -2和2 -2相同,允许心理弹性与学校适应各变量从第一年到第二年的自回归路径,以及心理弹性与学校适应各变量之间从第一年到第二年的双向预测路径; 同时,允许第一年时各个变量之间相关,允许第二年时各个变量之间的残差相关。为了控制初中生性别和家庭社会经济地位的影响,将初中生性别( 女孩= 0,男孩= 1)和父母文化程度( 小学=1,初中=2,高中=3,大学=4,研究生= 5,取父母的平均值) 作为协变量纳入到模型中,允许初中生性别和父母文化程度与第一年的5个潜变量相关,同时,设定初中生性别和父母文化程度对第二年的5个潜变量具有预测作用。用稳健极大似然法(MLR) 进行参数估计。
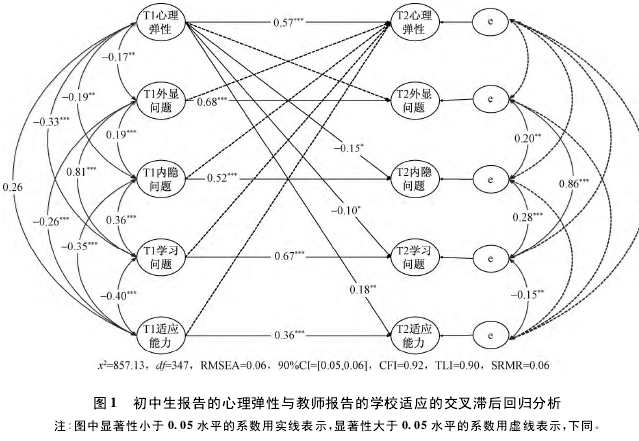
结构方程模型的结果显示,模型1 ~ 3的拟合良好。各观测指标的标准化因子载荷见表2,标准化的路径系数见图1( 图中未显示协变量部分结果)。从图1可以看出,在控制了初中生性别、父母文化程度以及心理弹性和初中生的学校适应各自的稳定性之后,第一年的心理弹性能够正向预测第二年教师报告的学校适应能力,负向预测第二年的内隐问题和学习问题; 第一年的外显问题、内隐问题和学习问题、学校适应能力无法预测第二年的心理弹性; 第二年时外显问题与内隐问题和学习问题残差之间具有显着相关,学习问题与内隐问题和适应能力的残差也显着相关。性别与第一年的心理弹性(r =﹣0. 11,p < 0. 05)、外显问题(r =0. 35,p <0. 001)、学习问题(r =0. 25,p <0. 001) 和学校适应能力(r =﹣0. 13,p < 0. 01) 显着相关,同时能够预测第二年的心理弹性(β =﹣0. 15,p < 0. 01)、外显问题(β = 0. 12,p < 0. 01)、学习问题(β =0. 15,p < 0. 001) 和学校适应能力(β =﹣0. 20,p < 0. 001) ,父母文化程度与第一年的心理弹性(r =0. 28,p < 0. 001)、内隐问题(r =﹣0. 16,p < 0. 01)、学习问题(r =﹣0. 15,p <0. 01) 显着相关。