曲线拟合模型建立与求解

　　摘    要：　纯理论性数学是创新的原动力, 而交叉学科的结合, 无异于是新世纪最大的突破, 不仅是打破了传统的学科禁锢, 还进一步解放了基础科学的生命力。本文基于药学案例, 运用数学建模思想, 提出问题、分析问题、解决问题这一思路, 直观展示曲线拟合数据分析技术。本文应用工具在各高校的开设课程中得到有利应用实践。

　　关键词：　曲线拟合; 分析技术; 数学建模;
 

　　1、 曲线拟合技术的应用

　　基础学科是创新型社会发展的原动力, 一个国家是否是属于创新型国家, 最重要的评判标准是该国家的基础科学创新发展是否强势。随着全球范围进入大数据开放时代, 不管是经济管理科学的研究, 还是物理化学等基础科学的演技都离不开数学。数学是一切学科的基础, 那么在数学的基础研究中可分为离散与连续两部分, 离散即是指研究的数据是无规律的, 而连续是可以用光滑的曲线链接起来的。

　　数学是建立的实际的基础之上, 即曲线拟合技术的成型早在其他学科早已发展成熟, 如常微分方程、偏微分方程、泛函分析、最值定理等领域。曲线拟合技术是否能数据能进行结合, 这一问题如何去解决, 可采取何种工具进行辅助。本文给出药学中案例, 结合数据分析软件, 进行实现曲线拟合技术的应用。

　　案例:某医院测定正常孕妇不同孕周GA (X) 羊水内的甲胎蛋白含量AFP (Y) 如表1所示。

　　表1 (孕周与AFP数据)

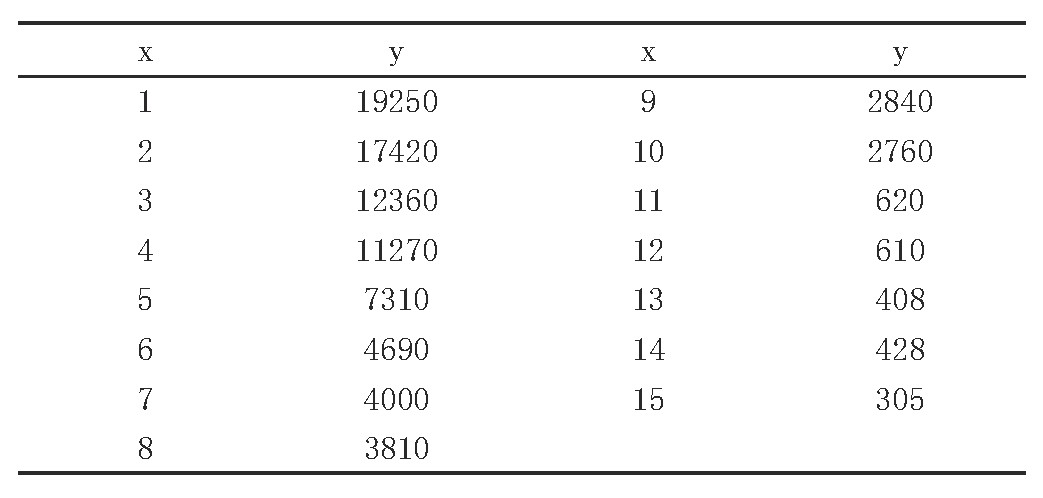
　　2、 曲线拟合模型建立

　　曲线即无数个点通过光滑的直线连接起来, 保证曲线是不间断。拟合即模型预期会出现的结果与实际的结果进行比对, 在有效的误差内, 无线接近我们想要的结果。本文曲线拟合模型如下:

　　3、 模型求解

　　利用统计学中散点作图原理, 我们采用SPSS进行作图得到结果如图1所示。

　　图1 散点图

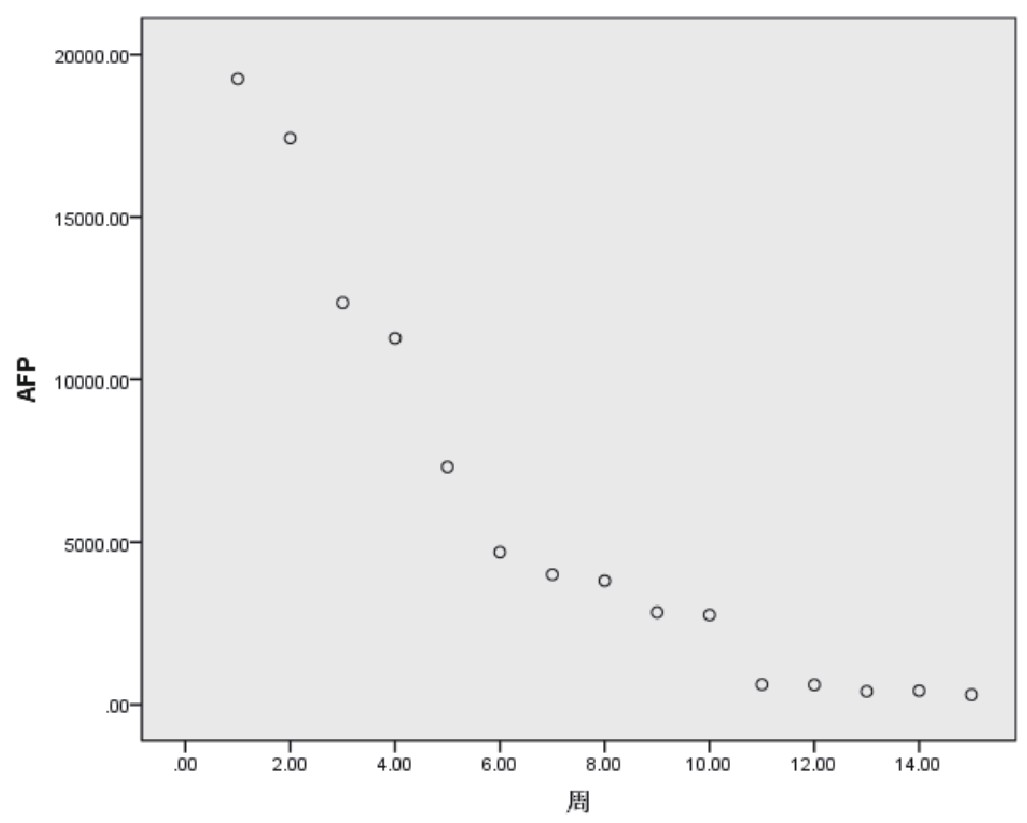
　　不难发现, 散点图的走势和指数函数, 多项式函数等表达式很接近。希望通过一条光滑曲线描述两者之间的关系, SPSS给出的曲线形式及对应图形, 经过分析, 可以得出, 本文的散点图和如下光滑曲线图接近。

　　因此利用多元统计分析的原理, 对数据进行处理得出结果如表2所示。

　　因变量:AFP

　　表2 (spss回归分析)

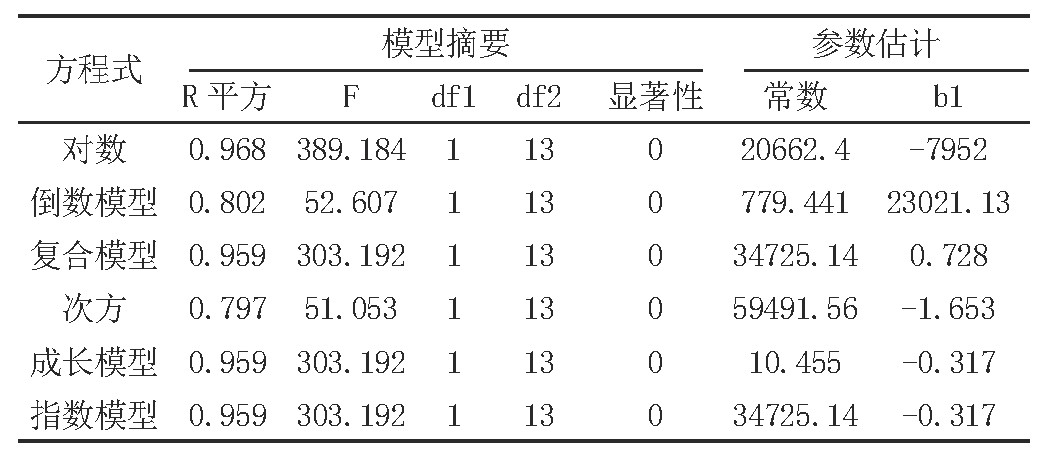
　　自变量为周

　　由表2可知道选择原则为:可决系数最大, 显着性检验P值<0.01, 系数值稳定。

　　得:

　　4、 模型的优化

　　根据模型的建立与求解的过程中, 发现拟合的函数表达式有很多, 即使根据可决系数, 显着性检验和系数值稳定等条件, 依然会出现多个表达式。那么这种情况是要选择优化数据和处理, 根据实际情况而处理。函数表达式的系数也决定了函数的灵敏度, 选择原则在不同的问题中根据数据最终结果来处理。

　　本文中案例的来源是科学, 理论上可选择对数模型或者指数模型, 根据泰勒展示也可以选择多项式模型。但数据的缺失和读取在一定程度上也决定了模型选择。

　　5、 结束语

　　统计学作为一门新兴的学科, 在未来的社会发展中有着举足轻重的意义。本文仅对医学上案例进行分析, 便可得到科学的分析, 也正迎合世纪科技的振兴, 使得数学建模的操作增添新的工具, 极大地提高了数据分析的科学性。

　　参考文献：

　　[1]陈岚峰, 杨静瑜, 崔崧, 等.基于MATLAB的最小二乘曲线拟合仿真研究[J].沈阳师范大学学报 (自然科学版) , 2014, 32 (1) :75-79.
　　[2]周浩.线性数据拟合方法的误差分析及其改进应用[J].大学数学, 2013, 29 (1) :70-76.
　　[3]吴文斌, 杨鹏, 唐华俊, 等, Shibasaki Ryosuke, 张莉.两种NDVI时间序列数据拟合方法比较[J].农业工程学报, 2009, 25 (11) :183-188+361.
　　[4]黄卓, 潘晓, 郭波.Phase-Type分布数据拟合方法综述[J].系统工程与电子技术, 2008 (11) :2167-2174.
　　[5]黄卓, 李苏军, 郭波.基于混合Gamma分布的通用可靠性寿命数据拟合方法[J].航空学报, 2008 (2) :379-386.
　　[6]牛常胜, 杨国为, 廖福成, 涂序彦.基于几何距离准则的新数据拟合方法[J].微计算机信息, 2006 (24) :151-152+163.