常用的数学建模软件及其应用探析

　　摘    要：　本文以MATLAB、LINGO软件在数学建模中的典型应用进行举例, 来体现MATLAB, LINGO等软件在建模过程中起到的关键作用。

　　关键词：　数学建模; MATLAB; LINGO;

　　一、数学建模定义及建模过程简介

　　数学建模重在解决生活问题, 将生活中出现的实际问题与其蕴含的内在规律, 用数学的思想方式和抽象思维把他们联系在一起, 通过数学公式的运用与数据的计算分析, 对数据进行整合。利用数学软件编程形成解决问题所需的数学模型, 再用模型进行对相关问题进行求解与分析, 得到合理的结果, 最后加以检验。建模的主要操作步骤如下: (1) 选取对应的模型 (2) 假设模型的建立条件 (3) 建立模型 (4) 利用模型求解问题 (5) 应用模型对结论进行检验。

　　二、常用的数学建模软件

　　数学软件是指能对数据进行分析, 对问题结果进行运算的软件, 它可以根据已有数据对将来的情况进行预测, 并有绘制图像的能力。数学建模软件大致上可分为大型平台软件和其他类型软件两类。本文将着重介绍MATLAB和Lingo。

　　Matlab是美国Mathwork公司研制的一个以矩阵计算为基础的科学和工程计算软件, 它的主要作用包括计算数据、符号整理、画图、预测结果以及应用工具箱。MATLAB最与众不同的是其语言的容易性。MATLAB是几乎人人都可以理解, 学会的建模软件, 他的编程语言十分简单易懂, 只需输入求解问题的数学表达式, 就可以得到运算结果。

　　LINGO是美国LINDO系统公司研制的一款主要解决最优化相关问题的软件, 它不单单可以计算出线性规划和二次规划问题的结果, 而且还可以计算非线性规划相关问题, 线性和非线性方程 (组) 的相关计算问题等。Lingo软件主要优势在于:语言通俗易懂, 计算十分准确、容易做出一些调整, 利于模型的建立和求解应用。

　　三、常用建模软件建模中的应用过程展示

　　(一) Matlab软件在建模实验中的应用举例

　　例1.某城市出现特大突发事故, 需要调度20个不同的交巡警平台的资源, 对进入该区的总共13条交通要道进行快速的封锁。根据现有的情况统计, 一个交巡警平台, 最多可以封锁1个路口, 请给出交巡警服务平台的最优调度方案。

　　数学模型构建:该问题是从20个交巡警平台当中选出13个平台, 对主要的13条要道进行封锁, 这13个平台到这13条主要的要道是最短的距离。对此, 可建立如下的0-1模型:

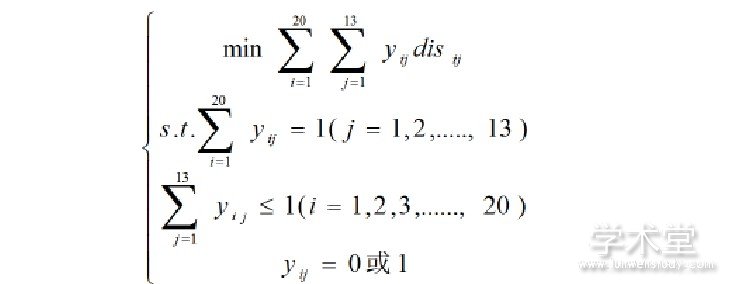
　　其中:表示第j个出口为某一个交巡警平台去封锁;

　　表示第i个交巡警平台去封锁13个要道中的1个。

　　通过上述的模型构建, 运用MATLAB软件进行编程, 从而可得到该调度的最优的解。

　　(二) Lingo软件在数学建模实验中的应用举例

　　例2.2006年全国大学生数学建模竞赛C题第二小题, 易拉罐是一个圆柱体, 圆柱的上底是a=0.026cm、下底是c=0.030cm、圆柱侧壁是b=0.014cm。我们考虑了易拉罐的外形设计问题, 建立相应的数学模型如下:

　　运行SOVLE, 得部分结果如下:

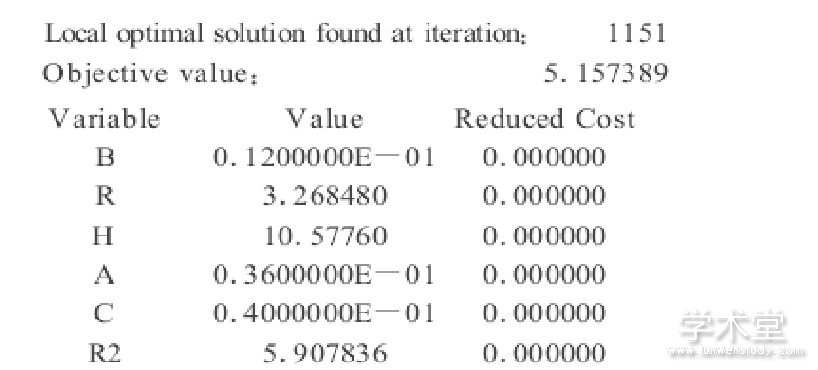
　　即底面半径是2.266540cm, 圆柱体高是8.47460cm时, 用料体积是7.157469时, 此时设计最优。

　　上例充分体现Lingo简单易学、方便快捷的优越性。

　　四、应用数学建模软件的意义

　　应用数学建模软件进行数学实验和建模是巩固和强化数学知识及应用, 满足了培养具有较高数学水平、较强创新能力和丰富实践经验的专业技术人才的需要。其在高校范围内的开展对培养学生数学学习兴趣, 强化数学应用能力和激发运用现代信息技术分析和解决实际问题的意识必将具有深远的意义。

　　参考文献

　　[1]任宪臻, 莫修明.matlab数据可视化在高等数学教学中的应用[J].数字技术与应用, 2012 (2) :172-173.
　　[2]温鲜, 霍海峰.Matlab软件在独立学院概率论与数理统计教学中的应用研究[J].大学教育, 2015 (10) :146-147.
　　[3]翁智峰.将MATLAB引入概率论与数理统计教学的探究[J].高教学刊, 2016 (11) :134-135.
　　[4] 薛定宇.高等应用数学问题的MATLAB求解 (第2版) [M].北京:清华大学出版社, 2006.
　　[5]梁浩云.数学软件在数学建模中的应用[J].数学的实践与认识, 2003, 33 (1) :111-116.
　　[6]赵静, 但琦.数学建模与数学实验 (第3版) [M].北京:高等教育出版社, 2008.