纸飞机飞行最远的抛出角度数学建模分析

　　摘    要：　本文首先研究纸飞机的飞行原理，结合伯努利定律进行受力分析，用Auto CAD软件绘制受力分析图，建立数学模型，从而得出纸飞机的最佳出手角度。采用控制变量法进行实验，并得出数据，绘制表格，进行记录，结合matlab软件，绘制飞行轨迹曲线，得出使飞行距离尽可能远的最佳方案，设计出手角度。

　　关键词：　纸飞机; 飞行原理; 数学建模;、

　　纸飞机自身没有动力，抛出瞬间获得一定初速度，机翼使空气分流，形成上下压力差，产生机翼的升力，升力与阻力合成为空气动力，维持纸飞机的飞行。机翼与机身的比例要恰当，合理调整纸飞机的重心、选择最佳出手角度等因素是纸飞机飞的高，飞得远的关键。

　　1、 问题重述

　　纸飞机有许多种折法，世界上有若干具有一定影响力的纸飞机比赛，通常的参赛规则是使用一张特定规格的纸，例如A4大小的纸张，折成一架纸飞机。折好后在无风的室内环境投掷，并测量其留空时间和飞行距离等成绩。我们假定纸飞机(以Suzanne为例)的翼面是精确的平面，需要建立合理的数学模型，计算出使飞行距离尽可能远，投掷出手的最佳角度。

　　2、 问题分析

　　通过对纸飞机受力分析，研究纸飞机的抛出角度

　　纸飞机属于无动力滑行的飞行方式，因此问题一需要根据伯努利定律，对纸飞机进行受力分析，研究纸飞机的受力情况，讨论气流遇到纸飞机时，如何被机翼分成上下两股气流，形成压力差从而产生升力。

　　3、 问题的求解

　　3.1、 伯努利定律在纸飞机上的应用

　　在空气动力学中伯努利定律最为重要，就是说空气流速越快，压强越小;反之空气流速越慢，压强越大。当空气遇到物体时会发生偏移，例如:纸飞机的机翼。当空气遇到机翼时，就会被分割成两部分，一部分从机翼的上表面流走，一部分从机翼的下部分流走。由于机翼的上表面比下表面凸出，所以上表面的气体流速比下表面的流速快，机翼的上表面压力比机翼的下表面压力小，产生压力差。两边相互较力，产生向上的推力，推动纸飞机向上。在这个流动过程中会产生复杂的速度和压力变化。要产生升力，上下表面的平均压力必须有差异。这个原理简单的数字表达式就是伯努利定律，以下式表示，其中p表示压力。
 

　　3.2、 气流对机翼的作用

　　气流遇到纸飞机时，被分为两股气流，流过机翼的上下表面，在飞机尾部汇聚成一股气流。根据伯努利定理，由于机翼上表面气流流速比机翼下表面流速小，造成机翼上表面的压力比下表面的压力小，造成压力差从而产生升力使飞机克服地球引力，达到飞行的目的。

　　3.3、 纸飞机受力原理

　　(1)动力来源:纸飞机属于无动力滑行的飞行方式，它只能依靠被抛出时所受的瞬间推力，上升到一定高度时依靠自身重力向前滑行。(2)阻力原理:阻力来源于空气对机身的摩擦力，为增进飞行效率，纸飞机在设计应尽量接近流线型，以减少阻力。(3)升力原理:升力来源于纸飞机的机翼与空气接触。其中影响升力的因素:空气浮力:流体对物体的浮力是由上下压力差而产生，相对于纸飞机来说，压力差不大(纸飞机机翼很薄，机翼的上、下面与空气的接触面几乎在同一高度)，因此假设可忽略不计。(4)牛顿第三定律(作用力与反作用力定律):对纸飞机的机翼做受力分析:抛出纸飞机时，一般都会与水平面成一定的夹角，斜向上投掷。此时机身与水平线的水平线的夹角称为攻角。空气会给纸飞机一个垂直于机翼的的力量，相对的机翼也会给空气一个反作用力，这个力量的垂直分力即为飞机的升力，水平分力成为阻力的一部分。

　　3.4 、纸飞机的受力分析

　　受力分析方程:

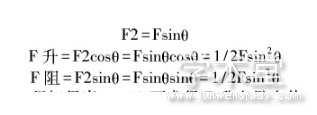
　　由上述方程解得当θ=45°可求得F升有最大值，当θ=90°时F阻有最大值，F升此时为0。

　　且此时F升=F阻

　　3.5 、用运动学知识建立最基础的纸飞机运动模型

　　若t=0时刻，纸飞机被抛出，抛出时的速度为v，抛出角为θ，纸飞机的飞行轨迹如图4所示，分析过程如下:

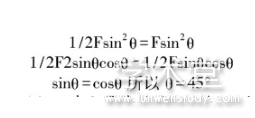
　　可得纸飞机的运动轨迹方程:

　　问题可转化为求(式1)式的极值问题:

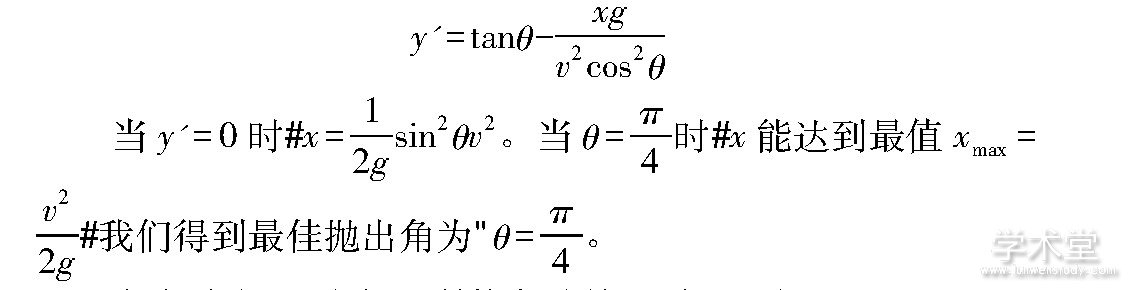
　　考虑升力、阻力与机翼仰角的关系，如下图所示:

　　机翼仰角与升力、阻力关系图

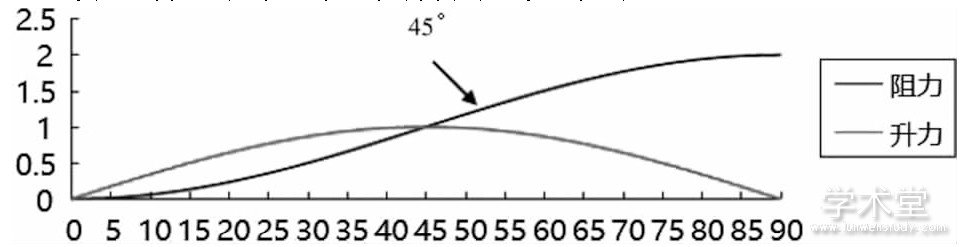
　　结论:当抛出角度为45度时，纸飞机的升力达到最大值，所以，抛出角为45度时，飞行距离会提高。

　　4 、总结

　　纸飞机的投掷方法:最佳投出角度约45°左右，选择最佳的纸飞机结构以及合适的投掷角度是纸飞机飞的高，飞得远的关键因素。

　　参考文献

　　[1] 贾跃华．纸飞机的原理．百度文库，2019-4-19.
　　[2]李炜璇．纸飞机．校园文范，2003.