4. 基于节点中心度和合着强度的文献检索可视化
4.1 节点中心度
通过上述内容的介绍,我们对于社会网络以及知识网络等都有了一个比较直观的理解。在对合着网络分析中,对合作关系强度的分析就是为了确定该作者在合着网络中的地位,即确定其在合着网络中的中心度。中心度的概念不仅仅存在于社会网络中,它是指各种网络的中心度,即确定各种网络中对应节点的重要程度。
在各种“网络”群体中,比如合着群体,在这个网络中我们可以分析在合着的研究成果中谁做出的贡献大,谁提出的意见好,谁做的研究起到了推动作用等。不免的要在该网络中对于每个合着人给出一番评价,这就是社会网络分析中的中心度分析。节点中心度也就是在群体中自己所占的位置以及自己所做出的贡献是否收到大家的认可,通过分析可以看到自己在群体中的是否占有中心地位等。对于节点中心度一般包括了点度、接近、中介中心度等。
4.1.1 节点中心度的概念
到目前对于节点中心度并没有一个比较明确的定义,在社会网络分析中一般用来说明一个人或者一个机构在一个群体中所起到的重要作用。这个节点能够对其他节点起到影响作用,其他节点的一些工作或者任务需要通过该节点进行管理和协助才能完成。该节点在群体中居于核心地位,其在权利、控制力以及领导力上发挥着重要作用。对于中心度的研究已经有非常多,对于各种中心度的描述以及分析我们通过下面内容进行详细介绍。
在计算中心度时,常常涉及到邻接矩阵的计算,在本实验中将邻接矩阵描述为:
假设在一个网络中 R 表示为对应的邻接矩阵,则 就用来表示节点 i、节点 j 之间的对应关系。如果节点 i、节点 j 之间有连接,则 为 1,否则为 0.在无向图中邻接矩阵是对称的,而对于有向图来说其邻接矩阵是不对称的,通常邻接矩阵主对角线上的元素都表示为 0.在加权网络中,邻接矩阵中的元素 表示的是相应的边的权重大小,而不是 0 或 1.
4.1.2 经典的节点中心度计算方法
通常用来表示中心度的方法有度中心度、紧密中心度和介数中心度。
1、度中心度
这种方法用节点的度来表示一个节点的中心度,度即一个节点连接其他节点的边的数目:
式中 n 表示一个网络中节点的总的数目; 表示第 i 个节点的连接边数。
在一个网络中,一个节点会与其他节点相关联,而它与其它节点的连接越多就说明它的度中心度越高,代表着其与其它节点的直接交互越强。这是一种直接的联系程度,不是间接的传递关系,因此一般用来度量中心度最简单和直观的方式就是度中心度。
2、紧密性中心度
在上述对于度中心度的介绍中已经把直接关系作为了一个指标来进行考虑,对于紧密型中心度则不一样,它考虑的是基于最短路径进行考虑的。其中,Freeman曾经说过,在网络中对于信息的传递来说,其他的节点必须要依赖于这个核心节点来进行传输。对于这个节点来说与其他节点的关系紧密程度越高,那么在发生信息传递的时候就无需依赖于其他网络节点。
紧密性中心度的计算公式是:
式中 表示节点 k 和 i 之间的最短距离。
紧密性中心度通常也就是我们说的紧密性,按照节点间的距离来进行描述中心度的大小,节点的中心度被表示为节点到其他各个节点的最短距离距离累和,但是通常也可以通过节点距离的倒数来表示该种节点的紧密程度。如果在该网络体系中,一个节点与其他的节点通过最短的距离建立的了联系,那么就可以从这个角度来说该节点已经具有了与其他节点很高的紧密度,这里重要的是最短连接路径,而不是关注节点间是否直接相连接。这个时候如果要在网络节点中传递信息,那么该节点的传播能力是最强的、也是最快的。
因此,对于上述介绍的合着网络群体来说,如果把合着者作为节点来分析,其中一个合着者与其他合着者之间的关系路径和最短,那么他就是这个合着群体中具有较高紧密性中心度的一位。如果由他来进行全体调度,协调工作,那么就会取得非常明显的效果。
3、介数中心度
介数是介数中心度的简称,它表示对应节点在其他节点最短路径中的关键程度,具体计算方法如下所示:
式中 表示节点 i、j 之间的最短路径经过节点 k 的路径数目; 表示节点i、j 之间的最短路的数目; 表示节点 i、j 之间的最短路径经过节点 k 的概率。
介数中心度表示的是网络中关键节点的位置,网络中的信息流通主要是通过介数中心度值高的节点来完成。
该种描述可以概括的来说就是群体中某个节点在其他节点与另外一些节点建立最短路径的关系时都经过了该节点,那么这个点被经过的频率就可以描述其介数中心度。这个概念说明了该中心点就像是一个中介或者一个中心机构,去其他的地方都必须要经过这个位置。因此这个节点非常重要。如果通过这个节点来传输信息或者发布消息,将会起到立竿见影的效果。
4、加权综合中心度
上面三种中心度算法都是常用的中心度算法,但是单一的使用某种中心度算法很难判断出节点之间的细微差别,有一定的不足之处。例如:对于度中心度,如果一个节点的度中心度很高,但它连接的其他节点都不重要时,这个节点的重要程度也会降低。对于介数中心度,所有只和一个点相连的点的介数中心度都为 0,如果这样的节点很多的话,就没办法精确的判断出节点的重要性。
本文提出了一种加权综合的办法来计算中心度,对每一种中心度都赋予一定的权重,综合考虑这三个指标:
从表中可以看出,三种传统的中心度算法都是从各自的角度来判断节点重要性,度中心度计算的是节点连接边数,紧密中心度计算的是节点在社会网络中的中心程度,介数中心度反映了节点在网络中处于关键路径上的概率。它们都可以判断出节点的重要性,但是不能判断出节点之间细微的差异性。加权中心度综合三种中心度的特点,对三种中心度中相同数值节点的判断给出了依据,并且节点排序符合三种中心度算法排序的综合趋势,全面的考虑了节点在网络中的重要性,解决了算法单一性的缺点。
4.1.4 基于中心度的文献检索可视化
对作者共引可视化,文献共引可视化,期刊共引可视化和共词共引可视化计算其中节点的加权中心度,对数据进行处理,计算结果后,取加权中心度大的对应值显示。
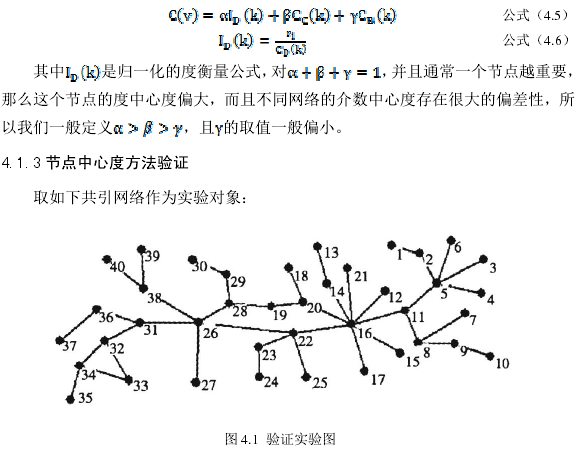
根据加权中心度值的排序,我们对数据进行筛选后,进行可视化,我们取排名靠前的给予显示,可视化图显示如下:
在上图中,节点属性值显示的大小跟其中心度值相对应,中心度值越大的节点,其属性值显示值就越大,而且在图中也可以看出作者文献间的共引关系,我们不难看出周宁,CHEN C,赵国庆,邱均平等人其文献被别人引用的最多而且他们自己的文献之间互引也比较频繁,这就反映出这他们是可视化方面的领军人物,这些人的文章在可视化方面很有参考价值,可视化的学习者们可以优先选取他们的文章进行学习。
在上图中,我们可以看到经过筛选后的文献共引可视化图,由于文献名较长,节点值显示的时候只显示了作者名字和出版年份,当鼠标点击相应的节点的时候可以看到相应文献名的具体信息,我们可以看到(赵国庆,2005,知识可视化的理论与方法,开放教育研究;陈超美,2009,科学文献中新趋势与新动态的识别与可视化,情报学报;周宁,2004,信息提供的可视化研究,情报科学等)文献被引用的次数较多,而且这些文献之间也存在互引关系,这些文献可以作为可视化方面的经典文献,适合可视化读者学习。
上图是筛选数据后的期刊共引可视化图,上图反映出了在可视化方面,情报学报,情报科学,Journal of theAmerican Society for Information Science and Technology,中国图书馆学报,计算机工程等期刊的引用较多,同时在一定程度上反应了这些期刊上的可视化文章相对有很高的参考价值,为可视化读者阅读提供了一定的方向。
经上图的共词可视化显示,我们可以看出,可视化的文章主要集中在可视化,信息可视化,可视化分析,知识图谱等研究领域,展示可视化学科领域中主题之间的关系,对可视化学科的结构研究,探索这个学科的发展趋势和研究热点很有帮助。
4.2 合着关系强度
社会是一个复杂的群体,在社会网络中存在着各种各样的关系,如相互合作、相互交互的关系,对于关系就有了强弱之分。这种关系的强弱可以用关系强度来进行说明,在网络中表示为边的权重。
在该理论的研究中比较着名的是 Granovetter(1973)弱关系理论,在该理论中其对于关系强度进行了分析,他对其分为了强关系和弱关系。在关系要好的亲友之间的关系就是强关系,在一般熟人关系之间的关系就是弱关系。对于一个人来说强关系非常重要,这些强关系形成了一些群体,这些群体的个体之间有着千丝万缕的联系。而对于弱关系来说,在这其中扮演了穿针引线的作用,通过这些弱关系使得不同的子群又发生了关系,弱关系是的整个网络成为了一个连通的整体。因此,如果一个成员想要获得关系网中相对位置远的信息,就必须拥有大量的弱关系网络,否则,他就只能接触到小范围的,仅限于亲密关系中的信息。在日常生活中也是这样,如果一个人只生活在自己的亲密圈子里面,那么对于外面的事务了解的很少。
当他认识很多可以穿梭于其他群体的熟人时,那么他获得的信息就非常丰富。
此外,对于这种关系强度 Newman 就文章的合作提出了自己的想法,如果一篇文章由很多个作者共同完成,那么很可能其中一些作者只是和某一部分作者合作的多,而和另一些合作的少,甚至不认识。因此,影响合作关系强弱的两个关键因素就是两个作者之间共同发表的文章数、每篇文章的作者数。后来 Borner 等人又在上述理论的基础之上进行了完善,指出这种合作关系强度还需要把合作文章被引用的次数加到里面来进行计算,这就开辟了另一个观点,就是说对于关系强度的度量还要包括合作者的合作成果所形成的社会影响力。
通常使用 Salton 算法和 Jaccard 算法来计算地区之间或者国家之间的合作关系强度。它们将地区与地区之间或者国家与国家之间合作完成研究成果的次数和它们各自完成科研成果次数的比值大小来判断两个地区或国家之间的合作关系强弱。
4.2.1 合着强度算法介绍
1、Newman 算法
该算法主要从合作文章数以及作者数之间的关系上进行了关系强度的分析,如果合作的多那么就说明合作者之间的关系密切,关系强度就高。有时候一篇文章由很多作者完成,一些作者可能只和其中某些作者合作次数多,其他作者甚至两两之间都不认识,因此 Newman 把影响合作强度的两个关键因素归结为合作作者共同发表的文章数和每个作者单独发表的文章数。下面给出合作强度的计算公式:
这个度量合着强度的算法主要用来描述两个国家或者地区合作的紧密程度,通过两个国家或地区合作文章的多少以及分别与各自在本地域发表的数量进行比值的比较来说明两个地区或国家紧密性,如果比值越大就说明这两个国家或地区的合作关系越紧密,反之就越弱。目前这两种方法在很多领域都在使用,并且很多专家对其进行了算法的改进,使其计算更具合理性。同时,通过这些统计可以对于一些区域之间进行较好的对比性,从而体现出地域特色。
3、基于 Salton 方法的合作关系算法
通常只考虑合着作者间合作次数的方法具有一定的局限性,例如如果 A 和 B合作完成了 3 篇文章,A 和 C 同样合着完成了 3 篇文章,但是 A 一共发表了 10 篇文章,B 一共发表了 7 篇文章,C 一共发表了 3 篇文章,明显可以看出 A 和 C 的合作强度要高于 A 和 B 的合作强度,这时候就不能用合作次数来评价合作强度。因此在这里提出了基于 Salton 方法的合作关系算法。
在上述中,我们对于 Salton 算法进行了描述,该算法适用于描述两个国家或者地区合作的紧密程度,通过两个国家或地区合作文章的多少以及分别与各自在本地域发表的数量进行比值的比较来说明两个地区或国家紧密性,如果比值越大就说明这两个国家或地区的合作关系越紧密,反之就越弱。其实,这种理论可以进行进一步的拓展,我们可以把这个两个国家或者地区进行缩小,将他们看成是合着网络中作者合着情况。这样就能够用此算法来计算合着网络中作者之间的合作关系强度。
基于上述分析,我们可以将计算合着网络中作者之间的合作关系强度的公式表示为:
的文章的数目用 表示;作者 i 和作者 j 各自发表的文章数分别用 和 表示。
在现实生活中实际上两个国家的合作也是通过具体的两个国家的几个科技工作者或者学者进行合作最终实现了对于两个国家成果的贡献,但其本质上还是学者之间的合作。因此,可以将两个地区多个作者间的合作看作是两个作者间的多次合作。该算法在计算方法上显得更为合理,比 Newman 考虑的因素更多也更为完善。
在 Newman 算法中对于合着过程中合作强度平均分配的缺点,在 Salton 方法进行了完善,从而使得对于关系强度的比较更为合理。
4.2.2 基于合着强度的合着关系可视化
对合着作者和合着机构分析生成基于 Salton 方法的矩阵后,用社会网络分析算法映射为如下可视化图:
从上图可以看出,在可视化共着方面,形成了分别以周宁、邱均平和刘则渊等人为中心的合作群体。由于研究成员的聚集,形成热点研究方向。从一方面为了揭示了可视化内在的结构演变状况,从而在一定程度上揭示出该学科研究的前沿。
同样我们从上图可以获知,在可视化研究方面形成了以武汉大学信息资源研究中心、中国科学技术信息研究所、中国科学院国家科学图书馆等研究机构的合作群体。参考这些科研机构在可视化方面的文献,可以在很大程度上提高我们对可视化方面的学习。
4.3 本章小结
本章在介绍了分析社会网络中节点中心度和合作强度的作用后,分析说明了相应的节点中心度与合作强度算法,用相应的算法对数据进行了处理,优化了作者共引、文献共引、作者合着、科研机构合着等可视化效果,从可视化图上可以方便看的看出相应的信息,使文献检索者对相应的科研领域能有初步的了解,方便读者检索相对应的文章,在一定程度上提高了人们的检索效率。