处理骨软骨栓的液相线跟踪法方案探析,医学工程论文

　　引言

　　软骨移植是临床上修复、重建和替换受损关节软骨的有效手段，捐献的软骨若能长期保存，那么外科医生将可针对病变部位挑选合适的移植物，并且有充裕的时间进行多项检测，以防止供者可能带来的病毒或细菌感染，这不仅有助于提高软骨移植手术的成功率，而且使得软骨移植手术的广泛开展成为可能[1,2].玻璃化保存是一种很有希望实现关节软骨长期保存的技术，到目前为止，关节软骨玻璃化保存的研究虽已取得了相当的研究成果[3 -5],特别是近来 Jomha 等报道他们玻璃化保存人关节软骨获得了 75%的软骨细胞存活率,但要真正应用于临床移植，细胞存活率仍有待进一步提高。玻璃化法实施的难点是如何把高浓度的低温保护剂载入生物材料，以及突破样品实际降温和升温速率的制约。Pegg 等利用低温保护剂毒性随温度降低而降低的特点，提出一边降低温度一边将二甲亚砜载入关节软骨，并始终使温度略高于组织冻结点的方法，最终使关节软骨内二甲亚砜达到近 60% （ w/w）的高浓度，如此高浓度的二甲亚砜也使得实现玻璃化和避免反玻璃化与所需降温和升温速率无关。

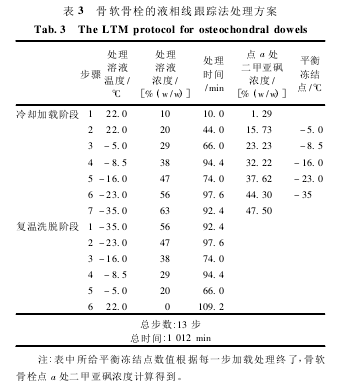
　　他们用此玻璃化法保存羊关节软骨获得了很大成功，并将其命名为 “Liquidus-tracking method（ LTM） ”[7],文中将其译成“液相线跟踪法（ LTM） ”.Pegg 等的 LTM 方案是针对特定尺寸（直径 6mm、厚约 1 mm）的不带有软骨下骨（ subchondralbone）的羊关节软骨片而提出的，而临床上软骨移植物的一般形式为带有软骨下骨的骨软骨栓（ osteochondral dowels） .Pegg 等的方案是否适用于骨软骨栓有待验证。本文采用数值分析的方法，先对现有的 LTM 方案用于处理骨软骨栓的可行性进行分析，然后以防止软骨组织内冰晶形成为目的，提出特定尺寸的骨软骨栓的 LTM 处理方案。

　　1 二甲亚砜渗透关节软骨数学模型二甲亚砜处理（加入/取出）关节软骨的过程主要为一扩散传质过程，笔者之前已建立了描述二甲亚砜渗透关节软骨的数学模型[8],此处只对模型作简要描述。

　　假设： 1）关节软骨不产生也不消耗二甲亚砜，不存在通过对流方式传递的二甲亚砜，不存在温度和压力梯度； 2）在处理过程中关节软骨不发生变形； 3）关节软骨为一多孔介质； 4）二甲亚砜在关节软骨中的扩散是各向同性的； 5）二甲亚砜在关节软骨中扩散的温度、浓度依赖性和非理想性与在单纯溶液中的相同； 6）忽略载入软骨细胞中的二甲亚砜的量； 7）处理溶液是由二甲亚砜和水组成的二元溶液； 8）将骨软骨栓样品看成是圆柱体，二甲亚砜无法从骨侧渗入/渗出软骨。

　　根据上述假设，二甲亚砜在关节软骨中的扩散采用下述连续性方程来描述：

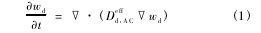
　　式中，Deffd,AC为二甲亚砜在软骨中的有效扩散系数，wd为二甲亚砜的质量分数，t 为时间。Deffd,AC采用下式计算：

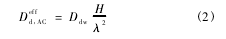
　　式中，Ddw为二甲亚砜在水中的扩散系数，H 为新鲜软骨含水量，λ 为软骨曲折度因子。对于二元溶液中的扩散，溶质在溶剂中的扩散系数等于溶剂在溶质中的扩散系数，于是有：Ddw= Dwd（ 3）式中，Dwd为水在二甲亚砜中的扩散系数。另外，对于二元溶液，各组分的互扩散系数与溶剂（本文指水）的自扩散系数存在如下关系：

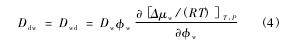
　　式中，Dw为水在二甲亚砜水溶液中的自扩散系数，w为水的体积分数，μw为水的化学势，R 为通用气体常数，T 为温度。式（ 4）中的 Dw可通过自由体积模型计算，即

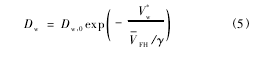
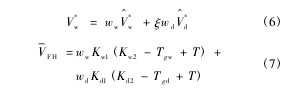
　　式中，Dw,0为指前因子，V*w为一个水分子从一个位置跳跃到另一个新位置所需的临界局部空穴自由体积，V-FH为每个分子的平均空穴自由体积，γ 为重叠因子，V^*w和 V^*1分别为水和二甲亚砜在 0 K 时的比体积，ξ 为水和二甲亚砜各自的跳跃单元的摩尔体积之比，ww为水的质量分数，Kw1和 Kw2为水的自由体积参数，Kd1和 Kd2为二甲亚砜的自由体积参数，Tgw和 Tgd分别为水和二甲亚砜的玻璃化转变温度。

　　参数 ξ 的表达式为：

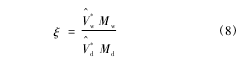
　　式中，Mw和 Md分别为水和二甲亚砜的相对分子质量。Dw,0与浓度有关，采用如下所示的二次多项式表达：lnDw,0= aw2d+ bwd+ c （ 9）式中，a、b 和 c 为常数。而式（ 4）中的[△μw/（ RT） ]T,P项可根据 Flory-Huggins 热力学理论计算，即：

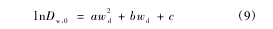
　　式中，y 为相对分子体积，#为 Flory-Huggins 相互作用参数，V^d和 V^ w分别为二甲亚砜和水的比体积。骨软骨栓样品为圆柱形，软骨下骨上方附着直径 D =6 mm、厚 H =1 mm 的软骨组织（见图 1） ,且软骨组织为各向同性、均匀一致的材料，故计算区.域取图 1 中矩形 abcd 即可。对于初始条件，假设新鲜骨软骨栓中不含二甲亚砜：wd（ z,r,t = 0） = 0 （ 12）式中，z 和 r 分别为轴向坐标和径向坐标。对于边界条件，假设二甲亚砜只可从顶面和侧面渗入软骨组织，而无法从底面（即骨侧）渗入，顶面与侧面的表面浓度等于周围处理溶液浓度（ ws）的 0. 9 倍

　　2 骨软骨栓的 LTM 处理方案

　　Pegg 等提出的针对直径 6 mm、厚 1 mm 的羊关节软骨片的 LTM 方案如表 2 所示[7].应用构建的数学模型对该方案处理同样软骨组织尺寸的骨软骨栓的可行性进行了数值分析，其中二甲亚砜溶液的平衡冻结点采用 Pegg 提出的公式[10]计算：

　　式中，tm为平衡冻结点温度（ ℃） ,S 为总溶质（二甲亚砜 + 氯化钠）的浓度（ g/100 g） ,A、B 和 C 为三个系数，分别为：

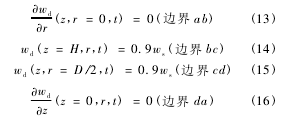
　　式中，R 表示二甲亚砜与氯化钠的质量之比。

　　如图 3 所示，在处理溶液温度低于 0℃ 的冷却加载步骤中，点 a 处（见图 1）的二甲亚砜浓度对应的平衡冻结点温度均要高于处理溶液温度，即骨软骨栓处于过冷状态，而且过冷度随着温度的降低而增大，最大达到约 30℃，冰晶将极有可能在软骨组织内形成。因此，对于骨软骨栓，需要设计新的处理方案。

　　模型的求解采用有限元法，所有计算均在COMSOL Multiphysics软件中实现，计算区域的网格划分如图 2 所示（经检验已足够密） .模型计算所需的参数值如表 1 所示[8].

　　表 3 为依据如下思路而建立的方案。

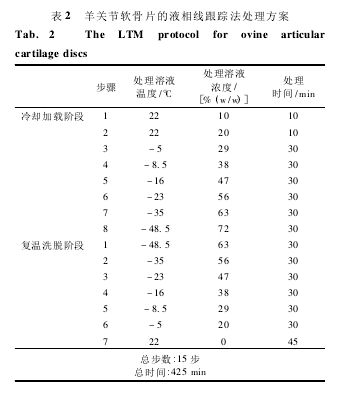
　　1）冷却加载和复温洗脱阶段各步的处理溶液温度和处理溶液浓度与现有方案的相同。

　　2）对于冷却加载阶段的某一步，当其接下来一步的处理溶液温度低于 0℃ 时，该步的处理时间应使得该步终了骨软骨栓点 a 处（如图 1）达到的二甲亚砜浓度对应的平衡冻结点温度等于接下来一步的处理溶液温度，即软骨组织不过冷。

　　3）当骨软骨栓点 a 处浓度达到 47. 5% （ w / w）时，冷却加载阶段结束[11].

　　4）假设当软骨组织内二甲亚砜的平均浓度降至 0. 1%（ w/w）时，复温洗脱阶段结束。

　　对比表 1 和表 3 可以看出，骨软骨栓的保护剂处理时间远远长于软骨片，其原因在于： 1）同样软骨体积的骨软骨栓相比于软骨片，可渗透表面的面积减少了 37. 5%; 2）骨软骨栓点 a 离可渗透表面的距离大于同样软骨厚度的软骨片中心点离表面的距离，即传质距离增大了。

　　对于传质面积减少、传质距离增大的骨软骨栓，传质阻力将是液相线跟踪法的重要制约因素，特别是在低温下。尽量减少二甲亚砜的载入量，对软骨内二甲亚砜的最终载入浓度进行优化研究，能够缩短 LTM 的处理时间[11].另外，也可以设法加速二甲亚砜渗透关节软骨的过程。对软骨这种特殊的受力组织，可以考虑采用周期性挤压法来强化传质过程：软骨片在被压缩的过程中排出存在于基质间的流体，在接下来的松弛过程中，软骨片在自身弹力的作用下逐渐恢复原状，在此过程中吸入周围的溶液。在生物力学领域，就有人通过周期性挤压法来加速化学物质在软骨内的渗透，如 Quinn 等采用周期性挤压法加速右旋糖苷的渗透[12].

　　3 结论

　　本研究应用二甲亚砜渗透关节软骨的数学模型，通过数值分析发现，当现有 LTM 方案应用于同样软骨尺寸的骨软骨栓时将产生较大的过冷度，冰晶将极有可能在软骨组织内形成，为此以避免软骨细胞在处理过程中遭受冰晶损伤为目标，提出了直径 6 mm、软骨厚 1 mm 的骨软骨栓的 LTM 处理方案，方案共 13 步，耗时1 012 min.本研究提出的处理方案以及方案的设计思路对玻璃化保存骨软骨栓的成功实施具有一定的指导和参考价值。