地方债对保险资金投资组合影响的实证分析

　　第4章 地方债对保险资金投资组合影响的实证分析

　　4.1 VAR 方法介绍

　　VAR 方法最早是由 JP Morgan 公司率先提出来的。VAR 的含义是处于风险中的价值（Value at Risk），表示在一定市场风险下某一金融资产或资产组合可能的最大损失。确切的说：在一定概率下（置信度水平），金融资产或证券组合在未来一段时间内的最大可能损失。数学上表示为：

　　

　　其中 Δp 为该金融资产在持续期 Δ t内的损失，VAR 为在置信水平下处于风险中的价值。我们可以假定某公司今年在 95%的置信水平日均 VAR 为 900 万美元，也就是说该公司可以在 95%的可能性下保证，某一时间点上，该公司的证券组合投资在未来24小时内因市场变化可能造成的损失不会超过900万美元。这是VAR含义的初步直观理解。更为精确的计算方法如下：

　　4.1.1 一般分布下的 VAR 计算

　　令 0p为资产组合的初始价值，r 是持有期内投资回报率，持有期期末金融资产组合的价值可以表示为0p = p （1 + r），其中令 r 的期望和波动性分别为μ和σ.

　　如果在某一置信水平下，金融资产的最低价值为* *0p = p （1 + r），则投资组合的VAR 可以表示为
 

　　从相对和绝地 VAR 的表达式看，我们可知，求 VAR 值实际上就是求资产或资产组合在一定水平下的最小价值*p或最小收益率*r .对最小价值*p或最小收益率*r 求解，可以采用蒙特卡洛模型或者历史法直接根据分位数求得，也可以利用参数法，根据收益率的分布，通过概率分布 f （ r ）求出。

　　我们假定未来收益的概率密度函数为 f （ r ），则给定了置信水平 c 后，投资组合的最低价值*r 满足：

　　

　　4.1.3 保险资金投资的单个 VAR 计算方法的选取

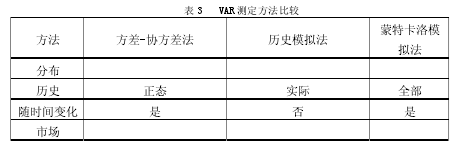
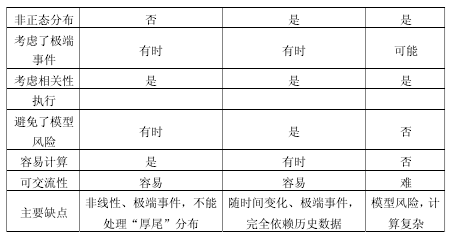
　　由上述的论述我们可以看出，计算 VAR 的关键是估计资产未来损益的统计分布或概率密度分布函数。不同的损益分布行函数对应的 VAR 方法也不同，我们熟知的主要计算方法有三种：方差-协方差分析法，历史模拟法和蒙特卡洛模拟法。我们可以对三种方法进行比较如下：

　　

　　从图表中可以得出，各类计算方法各有优缺点，并不一定存在一个完美的方法可以用于所有情况的分析，应该根据所研究的实际情况斟情选择恰当的方法进行研究。保险资金的投资属于机构投资者的范畴，而我们从已有的研究成果中可知，机构投资者投资收益具有非正态性，持有时间长，时变具有波动性的特点，这点我们在之后的实证中可以得出相应的结论。故而，在计算保险资金的 VAR时，我们偏向于选择历史模拟法进行计算。
 

　　4.1.4 VAR 方法的优势

　　目前，金融市场风险检测的主要方法除了 VAR 之外还有均值-方差分析法、灵敏度分析、波动性分析方法。

　　均值-方差分析起源于马克维茨的资产组合理论，该理论以均值和方差作为基本度量标准，均值用来衡量收益率，方差代表资产所受到的风险。

　　灵敏度分析是利用金融资产价值对其市场因子的敏感性来测量金融资产市场风险的方法。主要测量市场因子变化与证券组合价值变化间的关系，如 delta、beta、久期和凸性等，一旦得到这种关系，对于市场因子的特定变化量就可以求出证券组合价值的变化量。灵敏度分析的优点在于该方法简单直接，在实际中应用广泛。

　　波动性方法主要是分析资产主要是证券类的波动性，一般反应波动性的指标为方差和协方差，这两个指标估计了实际回报和预期回报的偏差。

　　以上三种风险测量方法各有优势，但是在实际中也存在明显缺陷，灵敏度分析不能很好的分析资产价格的变化，只是简单的反应了市场因子和证券资产之间的关系。波动性分析能得出资产实际收益与预期收益的偏离程度，但是不能测量出偏离的方向和偏离的原因，只能定性分析，不能定量分析。相较以上三种方法，VAR 方法是一种具有前瞻性的风险衡量方法，它基于金融资产过去概率分布，依据过去收益特征来进行分析资产价格波动性和相关性，在一定置信水平下估计最大可能损失。VAR 方法概念简单，便于理解，同时考虑了时间和概率的因素，可以事前计算风险，也可以衡量资产组合的整体风险，这有别于传统金融风险管理方法。基于这些优势，VAR 方法越来越成为金融风险管理中的主流方法，监管当局也开始运用 VAR 方法来确定风险资本。VAR 约束也开始代替方差标准差成为金融机构投资决策时考虑因素。

　　2009 年保监会出台的《关于规范保险机构股票投资业务的通知》中要求，"保险公司和保险资产管理公司应当加强基础建设，运用在险价值（VAR）等量化分析手段，按季进行股市风险压力测试，分析风险暴露程度，评估潜在风险因素及对整体风险承受能力",可见 VAR 方法得到了我国保险监管机构认可和推崇，故而，在本文的保险资金投资组合中，我们运用 VAR 方法替代最优投资组合模型中的方差来进行风险度量。

　　4.2 保险资金投资组合最优化模型

　　4.2.1 投资组合最优化理论与方法

　　最优化理论最初是起源于数学问题，最优化问题就是我们所熟悉的数学描述，在给定的条件下求出函数的极值点。最优化的理论逐渐发展至各个领域是与实践需求分不开的，在现实生活的各个领域，我们都希望和需要找到"最优"的解决问题方案，最优解成为人们普遍追求的目标，这点经济学也不能例外，我们找寻最优的生产成本，最优的投资组合，最优的资源配置等等，这些都是最优化理论在经济学上的运用。在金融学领域上的投资组合理论最早完善也被运用最广泛的是马科维茨的投资组合理论。

　　Markowitz 1952 年发表的《资产组合选择》，提出了着名的马科维兹资产组合理论，开创了不确定性条件下理性投资者进行资产组合和投资的理论方法。马科维兹的投资组合理论基于两个基本假设：投资者不满足性和投资者风险厌恶性。在这两个假设条件下，马科维兹选用资产的期望收益和资产方差分别作为资产收益的度量指标和风险度量指标。对于组合的预期收益和风险则用一下公式表示：

　　



 

　　其中ω 表示各资产投资比例，ijσ 表示两资产的协方差。由 4.8 和 4.9 确定的投资组合有效边界结合投资者无差异效用曲线能确定投资最优组合。马科维兹理论的主要思想贡献就是把量化思想引入了投资决策中，将投资组合的风险和收益用确定的数学量表示，是预期收益和风险有了具体的度量单位。

　　马科维兹的另一个重要思想就是我们前面提到的最优化思想，提出最优投资组合就是寻求收益最大化，风险最小化的投资策略。马科维兹的最优化方法就是在各资产投资比例之和为 1 的约束条件下，以投资收益最大化和风险最小化为目标函数，求解最优化问题的解。在数学上我们可以用以下方程组表示：

　　

　　公式中符号所表示的含义与 4.8、4.9 一致，其中第一式是收益最大化的表示公式，第二式是投资组合风险达到最小的表达式，第三式是表示投资资金在各个证券中进行分配，如果允许投资比例系数为负，则说明可以卖空某种证券，反之则说明不能对某种证券做空。

　　对于以上最优投资组合理论应用于保险投资我们也需要针对性的进行一些调整和修改，加入保险投资的特殊条件以使其更符合保险资金的投资组合。目前国内已有研究包括了一下主要修改方式：

　　（1）对目标函数也就是 4.10 中的第一式进行修改。保险公司的业务主要分为两个部分，承保业务和投资业务，两个部分构成保险公司主要受益来源，而且两部分也不是独立存在，故而，有一种研究保险资金投资组合的方法中，将保险公司的承保受益列入受益函数中，也就是在目标函数中加入保费收益。

　　（2）如我们前面所提到的，对 4.10 中的第二式进行调整修改，改变以往所使用的方差来表示投资组合风险，而用其他方法，如 VAR 作为衡量风险指标。

　　（3）一般来说，各国对保险资金投资与各资产都有相关法规限制，这也就要求了我们在考虑保险资金投资是后要加入政策对保险资金的投资比例限制因素，也就是对 4.10 式中第三式进行修改，对各部分的比例进行单独限制作为约束条件。

　　本文依然以马科维茨的投资模型为基础，得到保险资金的最优化模型，部分采用了上面所述的对模型的修改。

　　4.2.2 修正后的保险资金投资组合模型

　　通过以上的分析，我们初步建立保险资金投资组合的模型如下：

 

　　我们的模型考虑到保险资金的特殊情况作了写修改，同时也存在未尽完善的地方，如我们忽略了保费收入对保险资金投资收益的影响因素，这也是有本文所讨论的侧重点不在整体保险资金最优投资比例，而是针对性分析地方债对保险资金投资组合的影响，故而简化目标函数中的总投资收益函数是符合我们目标的。

　　4.3.数据来源及其运算

　　根据目前最新《保险法》规定，我国保险公司投资资产形式有：银行存款、债券、股票、证券投资基金等有价证券，投资不动产等国务院规定的其他资金运用形式。

　　2012 年 7 月 16 日中国保监会发布的《保险资金投资债券暂行办法》（保监发（2012）58 号）文件详细规定了保险公司投资债券的种类以及投资形式和方法。其中指出了"本办法所成债券，是指依法在中国境内发行的人民币债券和外币债券，包括政府债券、准政府债券、企业债券及符合规定的其他债券。"处于此考虑，我们可以把地方政府债券作为一个单独投资因素提取出来进行分析。

　　因此我们分别提取银行存款、股票、基金、国债、金融债券，企业债券和城投债作为我们模型中的各资产组合。我们选取数据时分别以上证指数、中债指数来代表保险投资中各资产的表现。上证综合指数是由上海证券交易所编制的，以上海证券交易所挂牌上市的全部股票为计算范围，以发行量为权属综合，反应了上海证券交易所的总体走势。我们以上证综合指数来代表保险投资中的股票投资，以上证基金指数代表证券投资基金，以上证国债指数代表政府债券（主要是国债），以上证企业债指数来代表企业债投资，中债金融债指数代表金融债投资。

　　特别的地方政府债券指数我们选取了上证城投债指数作为代表，相较于城投债指数，中债地方债指数更能代表我们所要研究的地方债特征，但是限于数据选取的困难，而且城投债一向作为准市政债券，我们以城投债指数作为地方政府债券指数来描述地方债的特征。

　　

　　故而，模型中的 i=1,2,3,4,5,6,7 分别代表银行存款、股票、基金、国债、金融债、企业债和地方债。

　　4.3.1 资产投资比例限制

　　保监会与 2014 年 4 月发布的《保险资金运用管理暂行办法》（保监令 2014年第 3 号）中修改了保险资金运用管理中对各个资产投资比例的限制，原 2010年发布《保险资金运用管理暂行办法》的第十六条为"保险集团（控股）公司、保险公司从事保险资金运用应当符合中国保监会相关比例要求，具体规定由中国保监会另行规定。中国保监会可以根据情况调整保险资金运用的投资比例。"我们依然运用原先的限制条件及参照国际标准，整理如下：

　

　　同时，我们也可以知道，保险公司不可能将所有资产都用于投资，上述的比列限制是针对保险公司总资产而言的限制，如投资于股票和股票基金的账面余额，不高于本公司上季末总资产的 20%,故而，我们需要对以上的数据进行调整。

　　我们由保险统计年鉴整理可以得出的是 2012 年 12 月末，保险资金运用余额 6.85万亿元，占总资产 93.2%,而 2011 年 12 月末保险也总资产为 6.013 万亿元，资金运用余额为 5.547 万亿元，保险资金可用余额占总资产的 92.2%,我们取两者平均值 92.7%,即把 0.927 作为调整系数。我们对保险法规对各资产的投资比例占总资产的限制调整为以保险可用资金为基数的比例限制。

　　

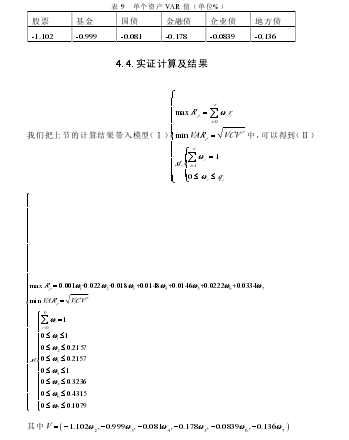
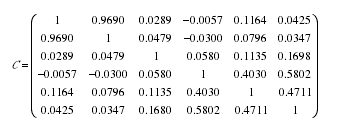
　　模型（Ⅰ）中的2q = 0.2157,3q = 0.2157,5q = 0.3236,6q = 0.4315,7q =0.10794.3.2 单个资产收益率计算。

　　单个资产期望收益率的计算我们选取代表各资产的指数日均收益率作为资产收益率。我们选取的样本为 2013 年 11 月 15 日到 2014 年 7 月 23 日期间各指数收益率的数据作为样本，共 165 个样本数据。

　　我们首先考虑银行存款利率，银行存款是为了满足流动性的需求，《保险资金运用管理暂行办法》中规定了保险资金银行存款必须不能少于上季度末总资产的 5%,我们在选取模型中银行存款利率的数值是选取 2014 年的各大银行货期存款利率的平均值来求得，如下表各商业银行活期存款利率：

　

　　从表 7 中我们可以看出，中农工建四大行是维持人民银行规定的基准利率水平上，即 0.35%的活期存款利率，而几个较大股份制银行则选取略高于基准利率的存款利率 0.385%的利率水平。综合考虑，我们选取两者的中间值作为我们模
 

　　得活期存款日均收益率为 0.001%.

　　对于其他资产，首先对各指数的每日收盘指数计算该资产的日收益率，然后对样本期间内的日收益率进行求均值，求得个资产的日均收益率值。

　　

　　4.3.3 单个资产的 VAR 值的计算

　　对于单个资产的 VAR 值的计算，我们采用前文提到过的历史模拟法进行计算，具体方法主要借鉴李毓在《金融风险的度量与管理》中介绍的。我们首先把样本中的收益率按照从大到小的顺序排列起来，然后用样本总数乘以分位数然后取整，该整数序号所对应的收益率就是该资产的 VAR 的数值。本文所选取的样本数为 165 个，我们取 95%的置信度，则排在 156 的收益率就是对应资产的 VAR值。该 VAR 表示的是资产收益率只有 5%的可能小于这一收益率。

　

　　我们可以看出，模型（Ⅱ）是一个双目标规划问题，存在两个目标函数：收益率函数和 VAR 函数，我们将 VAR 赋予特定值，把模型转换为单目标规划问题进行简化，本着控制风险的原则，我们将模型（Ⅱ）中的目标函数 VAR 转换为约束条件，即令保险投资组合的在险价值小于某一特定的损失率 p（p 为外置变量）。这样我们将模型转化为，在一定的规定在险价值范围内，保险资金的最优投资组合收益率达到最大时的投资结构。

　　这样问题就变成了一个非线性规划问题，运用 MATLAB 工具箱中的非线性规划求解可以求得在不同 p 值下的最优投资结构。

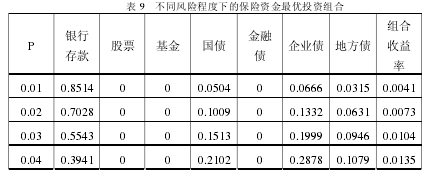
　　上表的数据表示意思是在某一规定的损失率下我国保险资金最优投资结构比例。如在保险公司可以承受的损失率在 4%的条件下，最佳的分配方案是银行存款 39.41%,国债 21.02%,企业债 28.78%,地方债 10.79%,此时的收益率为0.0135.从上表可以看出随着在险价值 p 值的变化，各资产的投资比例在相应变化，我们把上面模型（Ⅲ）中的7ω 去掉，得到没有地方债的投资组合模型。设定不同的 p 值得到不同风险水平下的保险资金投资比例：

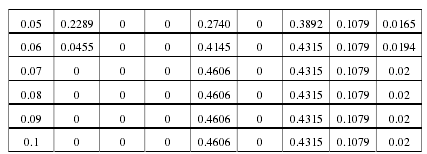
　　上表可以看出，在没有加入地方债的情况下，保险资金投资组合风险及其收益有些变化，在相对应的 p 值下，保险投资组合的投资收益率都略低于有地方债投资时的投资收益率。银行存款比例的变化与表 9 所示相同，都是在 p 值等于7%之后趋于零，也就是说在我们能忍受的风险损失率在 7%及以上时，银行存款的收益不足以满足我们所期望的风险补偿。与没有投资地方债相同，国债的投资比例虽说没有做限制，但在 p 等于 7%时也趋于一个固定的比例，企业债的投资比例在 p 等于 5%时达到我们设定的投资比例上限 43.15%.从上可知，保险公司所能容忍的资产投资损失为 7%,p=7%所对应的投资组合即为险资最优投资组合，此时建议的保险资金投资比例为国债 56.85%,地方债投资比例为 43.15%,对应的保险资金投资日收益率为 0.018%.

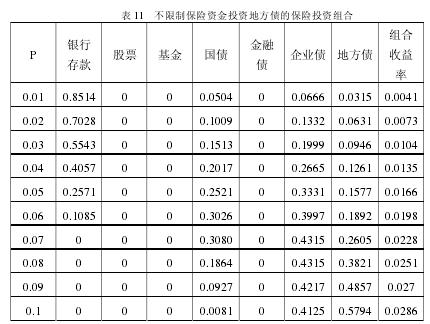
　　在模型（Ⅲ）构建中，我们设定了一个地方债投资比例限制，限制比例我们是参照国内外经验以及不动产投资的比例政策所确定的，在下面的分析中，我们假定对地方债的投资与国债投资一样，不设定投资比例限制，看看不设定投资比例限制，对保险资金投资组合的风险和收益率影响。

　　我们比较表 11 的结果和表 9 与表 10 的结果，不难看出在地方债放开限制后，其投资比例大有赶超国债的趋势成为投资比重最重的投资选项，而在相同的风险下，其收益率也要较约束了投资比例情况下高。在没有了地方债投资比例限制下，国债投资比例先随着投资收益率增加，到 p=7%之后开始转变，随着 p 值的变化变小，企业债也有相同趋势，但较之国债变化要小得多。而地方债突破了投资比例约束后，随着风险承受能力的提升，其在保险资金投资组合中所占比例变大，在 p=10%时甚至突破至 57.94%,占据投资比例一半之多，成为投资主体。