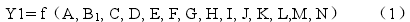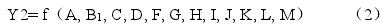第 4 章 教育补习的影响因素
4.1 教育补习机率的影响因素分析
为了探究影响高中生参加教育补习机率的影响因素,本文拟建构一个二分类变量(binary variable),用来反映学生参加课外补习的情况,如果学生选择没有参加教育补习,该变量赋值为 0,如果学生选择参加了教育补习,则该变量赋值为 1,在因变量为二分变量的情况下,常采用 logistic 模型。另外,已有的相关研究中也较多应用了这一模型,这就增强了本研究与以往研究的可比性。
因此,本文建立如下基本模型来分析影响教育补习机率的因素:
模型(1)中,Y1 是因变量,代表高中生是否参加了教育补习,为二分变量1 表示参与了教育补习,0 表示未参加教育补习;研究自变量的选取均提取于已有文献中的影响因子,其中,A 代表“城市类型”,B1代表“学校类型”,C代表“年级”,D 代表“班级排名”, E 代表“是否独生”F 代表“家庭收入水平”,G 代表“父亲学历”,H 代表“母亲学历”,I 代表“父母的有效指导”,J 代表“自己对学业的期望”,K 代表“父母对学业的期望”,L 代表“学生对补习的态度”,M 代表“父母对补习态度”, N 代表“性别”,在具体分析时,采用 Logistic 回归方程来探讨影响高中生教育补习参与机率的因素。
表 4.1 是 Logistic 的回归分析结果。Logistic 回归方程不能直接解释自变量变化对事件发生概率的影响大小,但可以分析其对事件发生的影响强度。一般而言,回归系数为正,事件发生概率将增加;回归系数为负,事件发生的概率将降低。本文将从四个方面对数据结论进行分析:
(1)学生背景
在研究选取的十四个影响因素中,“城市类型”、“学校类型”、“性别”、“年级”可放在学生背景中考虑。其中,“城市类型”分为县、地级市及省会城市,赋值分别为 1、2、3,从表 4.1 可以看出,家庭所在的城市类型对参与教育补习机率有显着的正影响,表明城市越大,则高中生参与教育补习的可能性越大;“学校类型”赋值重点高中为 1,普通高中为 0,如表 4.1 显示,学校类型的相关系数为正,回归系数通过了显着性检验,表明重点高中的学生参与教育补习的可能性比普通高中大;“性别”赋值男性为 1,女性为 0,结果显示性别对于参与教育补习的机率没有显着的影响,对应的显着性值大于 0.05,说明性别的差异并不会影响高中生是否参与教育补习;“年级”从低到高分别赋值为 1、2、3,从表 4.1 中可以看出年级对参与教育补习机率的影响显着性大于 0.05,表明年级对教育补习的参与率没有显着影响。
(2)家长背景
在所有的影响因素中,“家庭收入水平”、“父亲学历”、“母亲学历”这三个因素可归纳为家长的背景。研究将“父亲学历”和“母亲学历”划分为小学及以下、初中、高中和中专、高职和大专以及本科及以上,从低到高分别赋值为 1、2、3、4、5,从表 4.1 中可以看出,“父亲学历”和“母亲学历”回归系数均为正,且显着值均小于 0.05,说明父母亲的学历对高中生参加教育的机率有显着的正影响。换言之,父母的学历越高,孩子参与教育补习的机率越高。研究将“家庭收入水平”划分为五个等级,并从低到高分别赋值 1、2、3、4、5,如表 4.1 显示,家庭的收入水平对学生参加教育补习的机率有显着的正影响,表明家庭收入水平越高的孩子,参加教育补习的机率越大。
(3)学习现状
“班级排名”、“父母的有效指导”、“自己对学业的期望”及“父母对学业的期望”这四个影响因素可归于学生的学习现状中讨论。表 4.1 显示“班级排名”对高中生参加教育补习没有显着影响;为了探寻父母对孩子的有效指导是否会降低高中生教育补习的参与率,研究根据父母对孩子课业指导的程度分别赋值为 1、2、3、4,从表 4.1 中可以看出父母对孩子的有效指导对孩子参加教育补习的机率有显着的正影响,也就是说父母越能对孩子进行有效指导,越有可能让其孩子参与教育补习,对于这个结论,本文在第五章教育补习对社会关系的影响中所解释。研究将“自己的学业期望”和“父母的学业期望”分别赋值为 1、2、3、4,表 4.1 显示,“自己的学业期望”和“父母的学业期望”
回归系数均为正,且显着值均小于 0.05,说明学生对自己的学业期望越高,其参与教育补习的机率越高;同样,父母对孩子的学业期望越高,孩子参加教育补习的机率也越高。
(4)对待补习的态度
为了研究高中生的态度对教育补习参与机率的影响,研究根据学生是否同意“想要成绩好,就要参加教育补习”这个观点,赋值“是”为 1,“否”为 0,数据显示回归系数为正,且显着值小于 0.05,这说明学生对待教育补习的态度很大程度上决定了其是否参加教育补习。同样根据学生父母是否同意“成绩不好,就有必要参加教育补习”这个观点,赋值“是”为 1,“否”为 0,数据显示回归系数为正,且显着值小于 0.05,说明父母对待补习的态度对孩子是否参加教育补习有显着影响,值得注意的是,“父母对补习的态度”对学生参加教育补习的发生比为 7.655,远大于其他因素的发生比(发生比是指该自变量增加或者减少,因变量相应增加或者减少发生机率的倍数),换言之,父母对待补习的态度最有可能决定高中生是否参加课外补习。
4.2 教育补习支出的影响因素分析
4.2.1 相关分析
相关分析统计学中,pearson 相关系数是用来衡量两个定距变量间的线性关系。相关系数的值在-1 到 1 之间,其绝对值越大,表明两者的相关性越强。相关系数越接近于 1 或-1,相关度越强,反之则越弱。通常情况下当相关系数大于0.6 时,则能说明两者间有较强的相关性,pearson 相关系数大于 0 时,说明两者是正相关关系,反之则是负相关关系。
以下同样选取学生背景、家长背景、学习现状、对待补习的态度者四个方面的预测变量与补习支出做相关性分析,其中学生背景包括“性别”、“是否独生”、“城市类型”及“学校类型”;家长背景包括“父亲学历”、母亲学历“、”家庭收入水平“;学习现状包括”班级排名“、”父母对学业的期望“、”自己对学业的期望“、”父母的有效指导“;对待补习的态度包括”父母对补习的态度“和”学生对补习的态度“.
如表 4.2 所示:”性别“、”是否独生“与教育补习支出的相关系数低于0.3,并且显着值大于 0.05,说明这两个因素与教育补习支出没有显着的相关性。
”城市类型“、”学校类型“、”父亲学历“、”母亲学历“、”家庭收入水平“、”班级排名“、”父母对学业的期望“、”自己对学业的期望“、”父母的有效指导“、”父母对补习的态度“及”学生对补习的态度“等十二个变量与高中生教育补习支出有显着的相关性(相关系数大于 0.6,显着性小于 0.05)。
4.2.2 多元线性回归分析
根据以上的相关分析,我们已经找到与教育补习支出之间有显着相关性的变量,但是相关分析未考虑因素之间的混杂作用,并且相关性的因果关系未知,因此,研究在排除两个与教育补习支出无显着相关的变量的基础之上,为了进一步解释剩余12个因素对教育补习支出的影响,研究采用多元线性回归分析的方法,建立如下模型:
模型(2)中,Y2 代表参与教育补习的支出,为因变量;A代表”城市类型“,B1代表”学校类型“,C代表”年级“,D代表”班级排名“,F代表”家庭收入水平“,G代表”父亲学历“,H代表”母亲学历“,I代表”父母的有效指导“,J代表”自己对学业的期望“,K代表”父母对学业的期望“,L代表”学生对补习的态度“,M代表”父母对补习的态度“.
表 4.3 为线性回归分析的结果,方程中自变量的共线性检验值小于 10,表明自变量之间不存在严重的共线性问题。回归系数为正代表正影响,回归系数为负则代表负影响。本文同样从以下四个方面对数据进行解释分析。
(1)学生背景
研究将”城市类型“、”学校类型“及”年级“三个因素归类在学生背景中讨论。其中”城市类型“分为县级市、地级市、省会城市,赋值分别为 1、2、3,从结果中可以看出家庭所在的城市类型对教育补习支出有显着的正影响,表明城市经济发展水平越高,则家庭对孩子的教育补习支出越大。”学校类型“分为重点高中和普通高中,赋值分别为 1、2,从表 4.3 中可以看出,学校类型对教育补习支出没有显着的影响,对应的显着值大于 0.05;这与第四章中描述性的统计结果相悖,描述性统计结果显示,重点高中学生教育补习的支出大于普通高中。这也说明单纯的运用描述性的统计方法并不能准确的判定变量之间的影响关系。
(2)家庭背景
在研究选取的影响因素中,”家庭收入水平“、”父亲学历“和”“母亲学历”可归纳为学生的家庭背景。其中,“家庭收入水平”从低到高依次赋值为 1、2、3、4、5,从表 4.3 中可以看出,“家庭收入水平”对教育补习的支出有显着的正影响,换言之,收入水平越高的家庭对孩子的教育补习支出越高。
这与第 3 章中描述性统计的结果一致。研究由低到高对“父亲学历”和“母亲学历”依次赋值为 1、2、3、4、5,如表 4.3 显示,父亲和母亲的学历对教育补习支出有显着的正影响,表明父母的学历越高,其对孩子的教育补习支出就越高。
(3)学习现状
“自己对学业的期望”、“父母对学业的期望”及“父母的有效指导”这三个因素可归纳为学生的学习现状。表 4.3 显示,“自己对学业的期望”对所在家庭教育补习的支出有显着的正影响,表明学生自己对学业的期望越高,学生所在家庭的教育补习支出就越高。同样,从表 4.3 中可以看出,“父母的学业期望”对所在家庭的教育补习支出有显着的正影响,说明父母对孩子的学业期望越高,相对教育补习支出就越高。研究根据父母对孩子课业指导的程度对“父母的有效指导”依次赋值 1、2、3、4,从表 4.3 中可以看出,父母的有效指导对家庭教育补习的支出有显着的正影响,说明父母越能对孩子进行有效的指导,其对孩子教育补习的支出就越高。
(4)对待补习的态度
研究根据学生是否同意“要想学习好,就要参加教育补习”这个观点,赋值“是”为 1,“否”为 0,表 4.3 显示,学生对待补习的态度对家庭教育补习的支出有显着的正影响,表明学生对待教育补习的态度越积极,家庭对教育补习的支出就越高。根据父母是否同意“成绩不好,就有必要参加教育补习”这个观点,赋值“是”为 1,“否”为 0,表 4.3 显示,父母对待补习的态度对家庭教育补习的支出有显着的正影响,说明父母对待教育补习的态度越积极,家庭对于教育补习的支出就越高。
4.2.3 个案分析
对于教育补习支出的影响因素,统计结果显示:“城市类型”、“年级”、“家庭收入水平”、“父亲学历”、“母亲学历”、“自己对学业的期望”、“父母对学业的期望”、“父母的有效指导”、“学生对补习的态度”及“父母对补习的态度”等十个因素对家庭教育补习支出有显着影响。分析结果虽然如此,但研究者在调研的过程中仍发现一小类典型群体的存在:即所在城市经济发展水平低、家庭收入水平低、父母学历不高的家庭,他们反而不吝于对孩子的补习支出。于是,研究者想在此文中引入一个个案:
之所以引入这个个案缘于我一次对乐平市某中学零班教师的访谈,在得知我的研究结论后他建议我关注结论之外的典型群体,这位老师告诉我,虽然他们班上参加补习的同学大都是家里生活条件较优越的学生,但是仍有一位学生虽然家庭经济条件一般,但其父母却大力支持其课外补习。于是我就在元宵节后的一个中午在教室看见了王某,与同龄人相比,他看上去有些瘦小,对于我的来访,他感到有些意外,并且略有排斥,从他的表情中可以看出,桌上未做完的数学题远远比一个陌生人的闲聊来的有价值,毕竟高三阶段定是分秒必争的。
后经过我的一番自我介绍及来意的解释,特别是在得知我是在读研究生时,他一下对我敞开了心扉,他告诉我,自己也想考研,当然首先是要考个好的大学。他对我说,自己来自于乐平市众圤镇,父母曾是在家种地的,现都在外打工,如今他寄宿在数学老师家,由老师管理他的日常生活,并对他进行科目补习。“为什么不住寝室呢”我问道,“这是爸妈的意思,希望我能有老师的监管,住老师家,老师对我能关注一些,而且数学不懂的就能问,我觉得也很好”,“那每月的补习费多少呢”?他告诉我:“每个月一千五的费用,我爸妈在广州打工一个人也就两千块一个月,这笔钱已经是很大的开支了,而且我高中三年都是住在老师家”.“那你准备考哪个大学”,“我想考暨南大学,因为在广州,可以和爸妈在一起,一起分担”.我没有占用他太多的学习时间,互留了 QQ 号码就匆匆离开了。
后来我问他班主任要了他爸妈的电话号码,给他爸打了电话,他爸这样告诉我“他爷爷特别希望下一代能读出书来,可是那时候没钱,我也不争气,初中都没有毕业,所以我一定要让我的孩子读书,这孩子数学基础不好,还是感谢他老师能帮我带着他,这两次月考成绩都可以上二本线了,我跟他妈在外挣钱也挣的高兴,希望他能考上好的大学,可以当白领,有份体面的工作”.
他的数学老师这样告诉我:“类似于王某这样的农村孩子,他们对读书的认识程度会较高,加上他父母对他的期待值和他自己对自己的期待值都很高,读好书这个心理暗示的作用很大,学习很勤奋,补课的时候基本上是他问我答,非常有效率,成绩提高也很快。我也帮一些家里条件非常好的学生补过课,这类学生的理解力和智商很不错,父母也愿意投入,但学习目标不明确,补课很被动,我也很吃力”.
从这个个案中我们可以了解到,在参加教育补习的群体当中,也存在收入并不是很高的家庭,这类家庭对子女的学业期待值较高,“望子成龙”、“望女成凤”心愿迫切,这往往使他们不吝于对子女教育的投入,并试图通过这种投入来实现社会阶层的流动。而这类家庭的孩子,由于受父母态度的影响,对学习的认识程度相对于同龄人来说或许会更高一些,这类学生对待教育补习的态度往往是主动积极的,这也使得他们更容易在应试教育旗帜的引导下脱颖而出。当然,教育补习的群体中各种类型的典型都有存在,例如,我们在调研中还发现有一些收入较高、父母学历较高的家庭,家长却并不希望孩子参加教育补习,这类家庭已经拥有的社会经济地位使他们并不需要尽最大努力让孩子去迎合应试教育的浪潮,相反,他们或许更重视对孩子综合素质的培养。研究者在调研中发现,这类有悖于研究结论的小类典型群体仍有各类形式的存在。所以,对于教育补习影响因素的结论,我们或只能作为参考,不能生搬硬套。