基于LESLIE模型对儿童福利财政供给预测分析

　　第 5 章 基于 LESLIE 模型对儿童福利财政供给预测分析

　　5.1 儿童人口预测模型 LESLIE。

　　儿童人口的变化趋势是影响儿童政策实施的重要考量，因此，本文采用 LESLIE 人口预测模型对未来我国儿童人口变化趋势做基本预测。目前国际上有很多人口预测模型，包括曲线拟合、GM（1，1）灰色预测模型、基于 BP 神经网络预测模型和 Logistic预测模型等，但是经过修正的很多模型都是对总人口进行预测，不能针对不同年龄阶段对人口进行预测。为了儿童福利保障政策的实施更有效，达到福利效益最大化，需要对0-18 岁儿童人口进行预测，LESLIE 模型是澳大利亚学者 LESLIE 提出的一种模型，该模型主要起初主要用于分析动物种群数量变化，经过转化现在一般用于以年龄为机理的人口预测。

　　LESLIE 人口预测模型主要在于构造转移矩阵式（5-1）：

　　式（5-1）中，矩阵中ns 代表生存率，nb 代表生育率。LESLIE 模型中设定第 i 年的人口数就等于该年龄乘以对应的生存率。而第 i 年出生的新生婴儿数就是该年龄育龄妇女乘以对应的生育率，育龄妇女为 15 岁至 45 岁女性。然后基于模型对不同年龄的人口数量进行模拟预测。通过生育率和死亡率建立女性性别生命矩阵。即选取年龄间隔为 1岁的分组将 0-100 岁人口（100 岁以上包括 100 岁）的初始数量建立年龄矩阵式（5-2）：

　　式（3）中矩阵中的 S 表示对应年龄的存活率。那么00P S为 1 年后 0 岁人口的存活率，作为 1 年后 1 岁人口的组成部分。同样，通过各年龄段的生育率，可以构建出100*100 的出生矩阵式（5-4）：

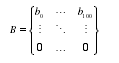
　　其中，第一行向量中非 0 数据为 15—49 岁育龄妇女的生育率，其他年龄的生育率均为 0。根据 S 矩阵和 B 矩阵构建 LESLIE 矩阵，L=B+S 式（5-5）：

　　5.2 儿童人口变化的计算机模拟。

　　5.2.1 儿童人口模拟。

　　本文在 2010 年第六次人口普查数据的基础上，建立 LESLIE 人口预测模型，在MSTLAB 仿真平台的基础上，对 2010 年到 2016 年人口预测数据进行仿真模拟，来验证这一模型的有效性，从而在决策系统中采用。

　　在仿真分析过程中，利用第六次人口普查的数据，根据各个年龄段的人数、死亡率和出生率，在 MATLAB 上编写预测人口的运行代码，预测的部分结果如表 1 所示。

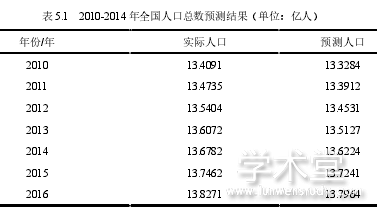
　　LESLIE 人口预测算法的优势在于，该模型考虑年龄结构、生育率和死亡率等多种因素，对人口发展进行动态的预测。通过 LESLIE 模型的建立，可以对每个年龄的人数进行预测，满足本文对儿童各年龄人口数量预测的需要。该模型也存在一定误差，测算数据小于实际人口数，可能与国家的相关政策有关，但总体而言，莱斯利人口预测模型在人口预测中取得了良好的效果，对于人口发展趋势提供一定的参考标准。

　　LESLIE 人口预测模型存在的误差主要是因为该模型中人口生育率和人口死亡率是重要的参数。而本文采用的是第六次人口普查的数据，即 2010 年人口的出生率和死亡率为参量。但是，随着社会的不断发展，生育率和死亡率是有所改变的，因此产生相应误差。该模型预测的人口增长速度明显快于实际人口的增长速度，所以应该计算参数，剔除影响因素，对人口预测数据进行修正。

　　基于模型的发展趋势，我们对原有的 LESLIE 模型进行改进，同样以全国人口为例，对测量结果添加了修正因子。在 MATLAB 仿真平台下，得到实际人口的误差平均值 r和预测的人口，并与莱斯利仿真预测的人口一起得到修正后的结果如表 5.2 所示。

　　从表 5.2 中可见，预测数据经过修正以后接近于实际人口数。最大误差绝对值减少到 0.001842。伴随着预测时间的延长，实际数据与预测数据之间的差距越来越大，每个人口结构数据的分布需要进行相应的修正。

　　5.2.2 预测结果分析。

　　从图 5.1 的预测结果显示，我国总人口呈不断上升的趋势，说明未来我国二胎生育政策会得到更好的落实，儿童人口数量会同步增加，有必要整体提高儿童福利财政供给。

　　虽然儿童人口总数有所增加，但是不同年龄段的儿童人口数量变化规模存在差异，现将儿童人口分 0-3 岁婴幼儿、4-6 岁学龄前儿童、7-12 岁小学儿童、13-15 初中儿童及未满18 岁高中学生，其人口变化趋势如图 5.3、图 5.4、图 5.5 及图 5.6 所示，所以根据不同的变化趋势，对不同阶段儿童福利投入的决策也应结合具体情况进行分析。

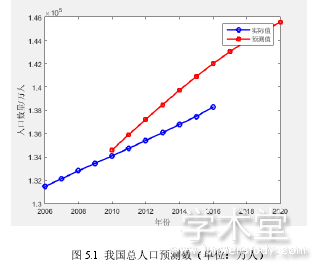
　　如图 5.2 所示，通过对 3 岁以前幼儿人口的预测，发现幼儿人口在 2011 年有很大的提升，与放开的“二胎政策”有直接关系，但由于当前生活压力较大，生育率在 2015年开始下降，预测在今后几年会持续下降，所以要适当减少私立幼儿园的数量，增加公立幼儿园的数量，重点优化区域学前教育机构布局，全面启动无证幼儿园的清理和规范工作。努力减少非分类幼儿园的覆盖率，使全覆盖幼儿园覆盖率达到 80%以上，等级幼儿园覆盖率达到 92%以上，建立覆盖面广、质量有保证的学前教育公共服务体系。

　　受“二胎政策”的影响，4-6 岁学龄前儿童在 2013 年之后达到最大值，如图 5.3 所示，之后呈平缓状态，财政要在现有投入基础上，适当增加幼儿的教育投入以及大病医疗投入。

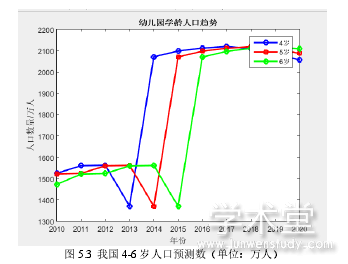
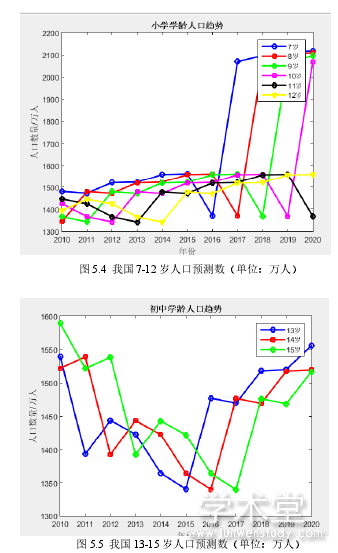
　　2010-2016 年，根据模拟决策系统的测算，全国人口的增长速度缓慢，因此，从人口规模来看，中国的人均 GDP 在中国 GDP 的稳步增长下不会显着下降。由此，学龄人口预测为义务教育决策提供了有效的数据支撑如图 5.4 所示，教育经费支持 2016 年有必要增加义务教育资源，来满足儿童教育供给，尤其是初中人口的增加需要大量的中学资源供给，财政要发挥其公共职能，以保证人口上升年份教育资源的有效供给，如图 5.5所示。

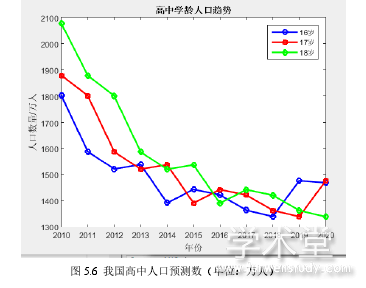
　　从全国范围来看，高中阶段学龄人口数（15 至 17 岁）会经历一个先下降后上升的过程如图 5.5 所示，未来对高中阶段资源的总需求在未来几年将呈现逐步下滑趋势，我们可以适当减少其财政供给，来满足学龄儿童不断上升的总需求。